题目内容
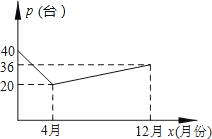
【题目】由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖,某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台.若一年内该产品的售价y(万元/台)与月份x(1≤x≤12且为整数)满足关系式:y=![]() ,一年后,发现这一年来实际每月的销售量p(台)与月份x之间存在如图所示的变化趋势.
,一年后,发现这一年来实际每月的销售量p(台)与月份x之间存在如图所示的变化趋势.
(1)求实际每月的销售量p(台)与月份x之间的函数表达式;
(2)全年中哪个月份的实际销售利润w最高,最高为多少万元?
【答案】(1)P=![]() ;(2)全年中1月份的实际销售利润w最高为8.75万元
;(2)全年中1月份的实际销售利润w最高为8.75万元
【解析】
(1)要根据自变量的不同取值范围,运用待定系数法分段计算出p与x的函数关系式;
(2)可根据实际销售利润=单件的利润×销售的数量,然后根据题目中给出的售价与月次的函数式以及(1)中销售量与月次的关系式,得出实际销售利润与月次的函数关系式,根据自变量的不同的取值范围分别进行讨论,然后找出最高售价.
(1)p=![]()
(2)①当1≤x<4时,
w=(﹣0.05x+0.4﹣0.1)×(﹣5x+40)
=![]() (x﹣6)(x﹣8)=
(x﹣6)(x﹣8)=![]() x2﹣
x2﹣![]() x+12
x+12
∵a=![]() >0,﹣
>0,﹣![]() =7>4,
=7>4,
∴当1≤x<4时,w随x的增大而减小,
∴当x=1时取得w的最大值为:
![]() ×12﹣
×12﹣![]() ×1+12=8.75 (万元).
×1+12=8.75 (万元).
②当4≤x≤12时,
w=(0.2﹣0.1)×(2x+12)=![]() x+
x+![]()
∵k=![]() >0,∴当4≤x≤12时,w随x的增大而增大,
>0,∴当4≤x≤12时,w随x的增大而增大,
∴当x=12时取得w的最大值为3.6:
![]() ×12+
×12+![]() =3.6 (万元).
=3.6 (万元).
综上得:全年中1月份的实际销售利润w最高为8.75万元.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目