题目内容
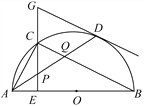
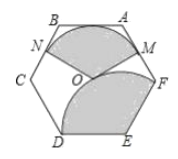
【题目】如图，点
为正六边形
的中心，点
为
中点，以点为圆心，以
的长为半径画弧得到扇形
，点
在
上，以点
为圆心，以
的长为半径画弧得到扇形
，把扇形的两条半径
重合，围成圆锥,将此圆锥的底面半径记为
；将扇形以同样方法围成的圆锥的底面半径记为
，则
=______．
【答案】
【解析】
根据题意正六边形中心角为120°且其内角为120°．求出两个扇形圆心角，表示出扇形半径即可．
解：连OA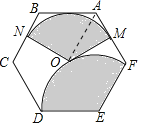
由已知，M为AF中点，则OM⊥AF
∵六边形ABCDEF为正六边形
∴∠AOM=30°
设AM=a
∴AB=AO=2a，OM=
a，
∵正六边形中心角为60°
∴∠MON=120°
∴扇形MON的弧长为：
，
则r1=
a，
同理：扇形DEF的弧长为：
，
则r2=
a，
r1：r2=：2.
故答案为：：2.
练习册系列答案
相关题目
