题目内容
 已知一次函数y=k1x-4与正比例函数y=k2x的图象都经过点A(2,-1)
已知一次函数y=k1x-4与正比例函数y=k2x的图象都经过点A(2,-1)(1)分别求这两个函数的解析式;
(2)求这两个函数的图象与x轴围成的三角形△OAB的面积;
(3)在y轴上是否存在点P,使△POB的面积是△OAB的面积的2倍?如果存在,请求出P点的坐标;如果不存在,请说明理由.
分析:(1)把点A(2,-1)代入一次函数y=k1x-4与正比例函数y=k2x中,求出k1、k2的值,即可得出这两个函数的解析式;
(2)根据直线y=
x-4,得出与x轴的交点坐标为(
,0),求出OB的值,再根据三角形的面积公式即可得出答案;
(3)根据三角形的面积公式得出S△POB=
PO•OB=
PO,当S△POB=2S△OAB时,求出PO=2,即可得出点P的坐标.
(2)根据直线y=
| 3 |
| 2 |
| 8 |
| 3 |
(3)根据三角形的面积公式得出S△POB=
| 1 |
| 2 |
| 4 |
| 3 |
解答: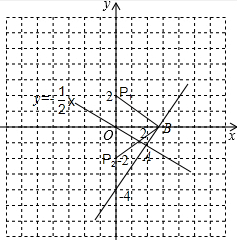 解:(1)∵一次函数y=k1x-4与正比例函数y=k2x的图象都经过点A(2,-1),
解:(1)∵一次函数y=k1x-4与正比例函数y=k2x的图象都经过点A(2,-1),
∴-1=2k1-4,-1=2k2,
∴k1=
,k2=-
,
∴一次函数的解析式为:y=
x-4,正比例函数的解析式为y=-
x;
(2)∵直线y=
x-4,与x轴的交点坐标为:(
,0),
∴OB=
,
∴S△OAB=
×
×1=
;
(3)∵S△POB=
PO•OB=
PO×
=
PO,
∴当S△POB=2S△OAB时,
PO=2×
=
,
∴PO=2,
∴点P的坐标为P1(0,2)或P2(0,-2).
 解:(1)∵一次函数y=k1x-4与正比例函数y=k2x的图象都经过点A(2,-1),
解:(1)∵一次函数y=k1x-4与正比例函数y=k2x的图象都经过点A(2,-1),∴-1=2k1-4,-1=2k2,
∴k1=
| 3 |
| 2 |
| 1 |
| 2 |
∴一次函数的解析式为:y=
| 3 |
| 2 |
| 1 |
| 2 |
(2)∵直线y=
| 3 |
| 2 |
| 8 |
| 3 |
∴OB=
| 8 |
| 3 |
∴S△OAB=
| 1 |
| 2 |
| 8 |
| 3 |
| 4 |
| 3 |
(3)∵S△POB=
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| 3 |
| 4 |
| 3 |
∴当S△POB=2S△OAB时,
| 4 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
∴PO=2,
∴点P的坐标为P1(0,2)或P2(0,-2).
点评:此题考查了一次函数的综合,用到的知识点是一次函数的图象与性质,三角形的面积公式,关键是掌握 三角形的面积与点的坐标的关系,注意结果有两种情况.

练习册系列答案
相关题目
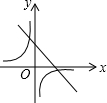
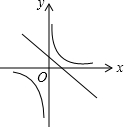
 (2013•连云港)如图,已知一次函数y=2x+2的图象与y轴交于点B,与反比例函数y=
(2013•连云港)如图,已知一次函数y=2x+2的图象与y轴交于点B,与反比例函数y=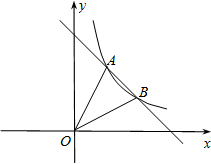 如图,已知一次函数y1=k1x+6与反比例函数
如图,已知一次函数y1=k1x+6与反比例函数 阅读下面的材料:
阅读下面的材料: