题目内容
已知一次函数y=k1x+b,y随x的增大而减小,且b>0,反比例函数y=
中的k2与k1值相等,则它们在同一坐标系中的图象只可能是( )
| k2 |
| x |
A、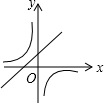 |
B、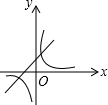 |
C、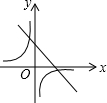 |
D、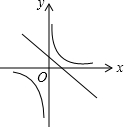 |
分析:根据一次函数的性质,y随x的增大而减小,则k1小于0,且b>0与y轴的交点在y轴的正半轴上,故A和B错误,反比例函数,y=
中的k2与k1值相等,k1小于0,则图象位于二、四象限.
| k2 |
| x |
解答:解:∵只有k<0时,一次函数图象y随x的增大而减小,
∴k1<0,
∴k2=k1<0,
∴反比例函数图象过二、四象限,
又∵b>0,
∴一次函数图象过一、二、四象限.
故选C.
∴k1<0,
∴k2=k1<0,
∴反比例函数图象过二、四象限,
又∵b>0,
∴一次函数图象过一、二、四象限.
故选C.
点评:根据一次函数和反比例函数的性质,一次函数y=kx+b,当k>0,y随x的增大而增大;当k<0,y随x的增大而减小.反比例函数y=
(k≠0),当k>0,函数的图象在一、三象限;当k<0,函数的图象在二、四象限.
| k |
| x |

练习册系列答案
相关题目
 (2013•连云港)如图,已知一次函数y=2x+2的图象与y轴交于点B,与反比例函数y=
(2013•连云港)如图,已知一次函数y=2x+2的图象与y轴交于点B,与反比例函数y=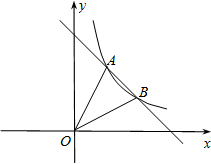 如图,已知一次函数y1=k1x+6与反比例函数
如图,已知一次函数y1=k1x+6与反比例函数 阅读下面的材料:
阅读下面的材料: