题目内容
【题目】平面直角坐标系xOy中，对于任意的三个点A、B、C，给出如下定义：若矩形的任何一条边均与某条坐标轴平行，且A，B，C三点都在矩形的内部或边界上，则称该矩形为点A，B，C的“三点矩形”．在点A，B，C的所有“三点矩形”中，若存在面积最小的矩形，则称该矩形为点A，B，C的“最佳三点矩形”．
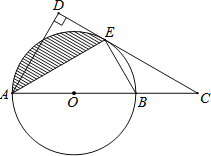
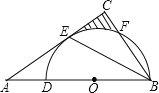
如图1，矩形DEFG，矩形IJCH都是点A，B，C的“三点矩形”，矩形IJCH是点A，B，C的“最佳三点矩形”．
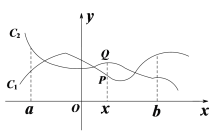
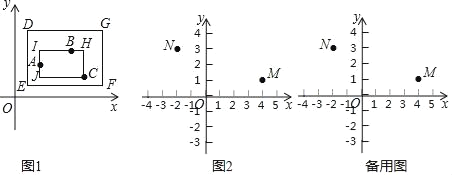
如图2，已知M（4，1），N（﹣2，3），点P（m，n）．
（1）①若m＝1，n＝4，则点M，N，P的“最佳三点矩形”的周长为 ，面积为 ；
②若m＝1，点M，N，P的“最佳三点矩形”的面积为24，求n的值；
（2）若点P在直线y＝﹣2x+4上．
①求点M，N，P的“最佳三点矩形”面积的最小值及此时m的取值范围；
②当点M，N，P的“最佳三点矩形”为正方形时，求点P的坐标；
（3）若点P（m，n）在抛物线y＝ax2+bx+c上，且当点M，N，P的“最佳三点矩形”面积为12时，﹣2≤m≤﹣1或1≤m≤3，直接写出抛物线的解析式．
【答案】（1）①18,18；②
或5；（2）①最小值为12，
；②点
的坐标为
或
；（3）
,或
.
【解析】
（1）①根据题意，易得M、N、P的“最佳三点矩形”的周长和面积②先求出
和
的值，再根据m=1以及M、N、P的“最佳三点矩形”的面积是24，可分析出此矩形的邻边长分别为6、4进而求出n的值
（2）①结合图形，易得M、N、P的“最佳三点矩形”的面积的最小值，分别将对应的值代入y=-2x+4即可求出m的取值范围②当M、N、P的“最佳三点矩形”为正方形时，易得边长为6，将对应的值代入y=-2x+4即可求出P点坐标
（3）根据题意画出图像，易得抛物线的解析式
解：（1）①如图，过P做直线AB平行于x轴，过N做直线AC平行于y轴，过M做MB平行于y轴，分别交于点A（-2,4）、C（-2,1）、B（4,1）
则AC=BM=3，AB=CM=6故周长=（3+6）
=18，面积=3
=18
故M、N、P的“最佳三点矩形”的周长和面积分别为18,18；
② ∵M（4,1），N（-2,3）∴
，
又∵m=1，点M、N、P的“最佳三点矩形”的面积为24
∴此矩形的邻边长分别为6，4
∴n=-1或5
（2）如图1，
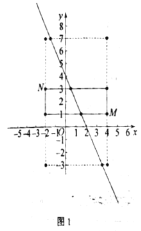
① 易得点M、N、P的“最佳三点矩形”的面积的最小值为12；
分别将y=3，y=1代入y=-2x+4，可得x分别为
，
结合图象可知：
②当点M、N、P的“最佳三点矩形”为正方形，边长为6，
分别将y=7，y=-3代入y=-2x+4 ，可得
分别为
，
点P的坐标为（ ，7）或（ ，-3）
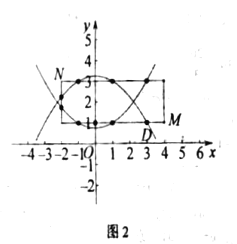
（3）如图2，y=
+
或y=
+
