题目内容
已知AD是△ABC的角平分线,E、F分别是边AB、AC的中点,连接DE、DF,在不再连接其他线段的前提下,要使四边形AEDF成为菱形,还需添加一个条件,这个条件可以是 ;
【答案】
答案不唯一,如AB=AC
【解析】
试题分析:菱形的判定方法有三种:①定义:一组邻边相等的平行四边形是菱形;②四边相等的四边形是菱形;③对角线互相垂直平分的四边形是菱形.
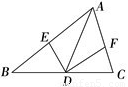
由题意知,可添加:AB=AC.
则三角形是等腰三角形,
由等腰三角形的性质知,顶角的平分线与底边上的中线重合,
即点D是BC的中点,
∴DE,EF是三角形的中位线,
∴DE∥AB,DF∥AC,
∴四边形ADEF是平行四边形,
∵AB=AC,
点E,F分别是AB,AC的中点,
∴AE=AF,
∴平行四边形ADEF为菱形.
考点:三角形的中位数定理,等腰三角形的性质,菱形的判定
点评:此类问题综合性强,注意考查学生对基本图形的性质的熟练应用程度,在中考中比较常见,在各种题型中均有出现,需多加关注.

练习册系列答案
相关题目
 于点F,连接FB、FC.
于点F,连接FB、FC. 3、如图,已知AD是△ABC的中线,AE=EF=FC,下面给出三个关系式:①AG:AD=1:2;②GE:BE=1:4;③GE:BE=3:4,其中正确的为( )
3、如图,已知AD是△ABC的中线,AE=EF=FC,下面给出三个关系式:①AG:AD=1:2;②GE:BE=1:4;③GE:BE=3:4,其中正确的为( )
