题目内容
【题目】先化简,再求值:(a+2b)2+(a+b)(b﹣a),其中a=2,b=﹣1.
【答案】解:原式=a2+4ab+4b2+b2﹣a2=4ab+5b2,
当a=2,b=﹣1时,原式=﹣8+5=﹣3.
【解析】利用平方差和完全平方公式,可化简得出结果.
【考点精析】根据题目的已知条件,利用完全平方公式和平方差公式的相关知识可以得到问题的答案,需要掌握首平方又末平方,二倍首末在中央.和的平方加再加,先减后加差平方;两数和乘两数差,等于两数平方差.积化和差变两项,完全平方不是它.

练习册系列答案
相关题目
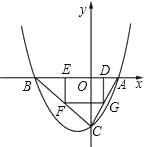
【题目】如图,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:
x | … | ﹣3 | ﹣2 | 1 | 2 | … |
y | … |
| ﹣4 |
| 0 | … |
(1)求A、B、C三点的坐标;
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并指出m的取值范围;
(3)当矩形DEFG的面积S取最大值时,连接DF并延长至点M,使FM=kDF,若点M不在抛物线P上,求k的取值范围.