题目内容
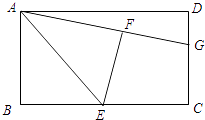
【题目】如图,ABCD的对角线AC、BD相交于点O,EF过点O且与AB、CD分别相交于点E、F,连接EC.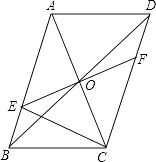
(1)求证:OE=OF;
(2)若EF⊥AC,△BEC的周长是10,求ABCD的周长.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴OD=OB,DC∥AB,
∴∠FDO=∠EBO,
在△DFO和△BEO中, 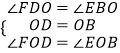 ,
,
∴△DFO≌△BEO(ASA),
∴OE=OF.
(2)解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OA=OC,
∵EF⊥AC,
∴AE=CE,
∵△BEC的周长是10,
∴BC+BE+CE=BC+BE+AE=BC+AB=10,
∴ABCD的周长=2(BC+AB)=20
【解析】(1)根据平行四边形的性质得OD=OB,DC∥AB,根据平行线的性质得∠FDO=∠EBO,然后利用ASA证出△DFO≌△BEO,利用全等三角形的性质即可得出结论;
(2)根据平行四边形的性质得AB=CD,AD=BC,OA=OC,然后根据中垂线的性质得AE=CE,根据三角形的周长得BC+BE+CE=BC+BE+AE=BC+AB=10,进而得出平行四边形的周长。
【考点精析】通过灵活运用线段垂直平分线的性质和平行四边形的性质,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分即可以解答此题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目