题目内容
【题目】如图,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.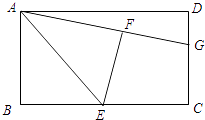
(1)猜想线段GF与GC有何数量关系?并证明你的结论;
(2)若AB=3,AD=4,求线段GC的长.
【答案】
(1)解:GF=GC.
理由如下:连接GE, 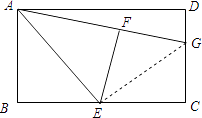
∵E是BC的中点,
∴BE=EC,
∵△ABE沿AE折叠后得到△AFE,
∴BE=EF,
∴EF=EC,
∵在矩形ABCD中,
∴∠C=90°,
∴∠EFG=90°,
∵在Rt△GFE和Rt△GCE中,
![]() ,
,
∴Rt△GFE≌Rt△GCE(HL),
∴GF=GC;
(2)解:设GC=x,则AG=3+x,DG=3﹣x,
在Rt△ADG中,42+(3﹣x)2=(3+x)2,
解得x= ![]() .
.
【解析】(1) GF=GC,理由如下:连接GE, 由中点定义折叠的性质得出EF=EC,由矩形的性质得出∠C=90°,∠EFG=90°,从而利用HL证出Rt△GFE≌Rt△GCE,根据全等三角形对应边相等得出结论;
(2)设GC=x,则AG=3+x,DG=3﹣x,在Rt△ADG中根据勾股定理列出方程求解即可。

练习册系列答案
相关题目