题目内容
【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
(1)求证:△ABE≌△DAF;
(2)若AF=1,四边形ABED的面积为6,求EF的长.
【答案】
(1)证明:∵四边形ABCD是正方形,
∴AB=AD,
∵DF⊥AG,BE⊥AG,
∴∠BAE+∠DAF=90°,∠DAF+∠ADF=90°,
∴∠BAE=∠ADF,
在△ABE和△DAF中,
 ,
,
∴△ABE≌△DAF(AAS).
(2)解:设EF=x,则AE=DF=x+1,
由题意2× ![]() ×(x+1)×1+
×(x+1)×1+ ![]() ×x×(x+1)=6,
×x×(x+1)=6,
解得x=2或﹣5(舍弃),
∴EF=2.
【解析】(1)根据正方形的性质得出AB=AD,又根据垂直的定义及同角的余角相等得出∠BAE=∠ADF。然后根据AAS判断出△ABE≌△DAF;
(2)根据全等三角形对应边相等得出AE=DF,设EF=x,则AE=DF=x+1,根据四边形ABED的面积=S△ABE+S△AFD+S△DEF列出方程求解即可。
【考点精析】利用正方形的性质对题目进行判断即可得到答案,需要熟知正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

 阅读快车系列答案
阅读快车系列答案【题目】电影《中国机长》是根据2018年5月14日川航3U8633航班的真实事件改编的,当时飞机挡风玻璃在高空爆裂,机组临危不乱、果断应对,顺利返航.下表给出了飞机距离地面高度![]() 与所在位置温度
与所在位置温度![]() 的部分统计数据,根据下表,请回答以下问题:
的部分统计数据,根据下表,请回答以下问题:
距离地面高度 | 0 | 1 | 2 | 3 | 4 | 5 |
所在位置的温度 | 20 | 14 | _____ | 2 |
|
|
(1)上表反映的两个变量中,________是自变量,________是因变量;
(2)用关系式表示上表两个变量之间的关系:________;
(3)如图是当日飞机下降过程中距地面高度![]() 与玻璃爆裂后立即返回地面所用时间
与玻璃爆裂后立即返回地面所用时间![]() 的关系图.根据图象回答以下问题:
的关系图.根据图象回答以下问题:
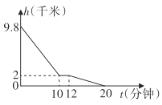
①返回途中飞机在2千米高空水平盘旋了几分钟?
②飞机盘旋时所在高空的温度是多少?