题目内容
已知⊙O的半径为2cm，弦AB长为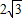
cm，则这条弦的中点到弦所对劣弧的中点的距离为（ ）A．1
B．2
C．3
D．4
【答案】分析：如图：连接OA，OB，则OA=OB=2cm．过O作OF垂直AB于E，与圆相交于F．根据垂径定理和勾股定理求解．
解答：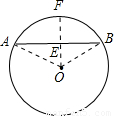
解：
如图：连接OA，OB，则OA=OB=2cm
过O作OF垂直AB于E，与圆相交于F
由垂径定理得AE=EB=
AB=
×2
=
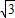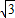（cm），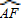
=
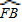
在Rt△OEB中，OB=2cm，EB=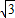
cm，OE=
=
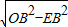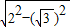=1
即这条弦的中点到弦所对劣弧的中点EF=OF-OE=2-1=1（cm）．
故选A．
点评：此题属简单题目，涉及到垂径定理及勾股定理的运用，需同学们细心解答．
解答：
解：如图：连接OA，OB，则OA=OB=2cm
过O作OF垂直AB于E，与圆相交于F
由垂径定理得AE=EB=
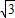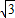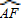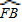
AB=×2=（cm），=在Rt△OEB中，OB=2cm，EB=
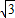cm，OE=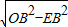==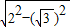1即这条弦的中点到弦所对劣弧的中点EF=OF-OE=2-1=1（cm）．
故选A．
点评：此题属简单题目，涉及到垂径定理及勾股定理的运用，需同学们细心解答．
练习册系列答案
相关题目
已知⊙O的半径为2cm，弦AB长为2
cm，则圆心到这条弦的距离为（ ）
| 3 |
| A、1 | B、2 | C、3 | D、4 |