题目内容
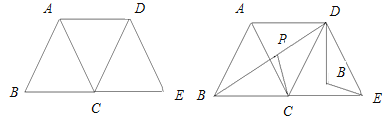
【题目】已知三个全等的等边三角形如图1所示放置,其中点B、C、E在同一直线上,
(1)写出两个不同类型的结论;
(2)连接BD,P为BD上的动点(D点除外),DP绕点D逆时针旋转60到DQ,如图2,连接PC,QE,
①判断CP与QE的大小关系,并说明理由;
②若等边三角形的边长为2,连接AP,在BD上是否存在点P,使AP+CP+DP的值最小,并求最小值.
【答案】(1)答案见解析;(2)①CP=QE,理由见解析;②存在,AP+CP+DP的最小值为![]()
【解析】解:(1)答案不唯一,合理即可,
如AD∥BE,四边形ABCD、ACED是菱形;
四边形ABED是等腰梯形;四边形ABED是轴对称图形;
 (2)①CP=QE;理由:
(2)①CP=QE;理由:
∵△AEC是等边三角形,
∴CD=DE,∠CDE=60,
∵DP绕点D逆时针旋转60到DQ,
∴PD=DQ,∠PDQ=60,
∴∠PDQ=∠QDE,
∴△DPC≌△DQE
∴CP=QE。
②连接AP,由①可知CP=QE,
∵DP绕点D逆时针旋转60到DQ,
∴△DPQ是等边三角形,
∴DP=DQ,
要使AP+CP+DP的值最小,关键是AP+QE+QP的值最小,即点A、P、Q、E在同一直线上(AE),构建两点之间,线段最短,过点A作AM⊥BE于点M,可得BM=1,EM=3,AM=![]() ,
,
所以AE=![]() ,
,
故在BD上存在点P,故AP+CP+DP的值最小,最小值是![]() .
.

练习册系列答案
相关题目