��Ŀ����
����Ŀ��һ��ֱ�����ǰ壨����һ�����ǰ���ڽ���45��,45��,90��,��һ����30��,60��,90����
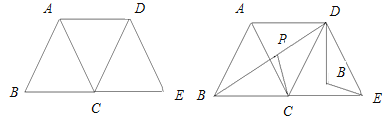
��1����ͼ�ٷ��ã�AB��AD,��CAE=_______��BC��AD��λ�ù�ϵ��__________��
��2���ڣ�1���Ļ����ϣ�����һ��30��,60��,90���ֱ�����ǰ壬��ͼ�ڷ��ã���AC���ߺ�AD���غϣ� AE�ǡ�CAB���Ľ�ƽ����������ǣ������˵����������ǣ���˵�����ɣ�
��3�����ݣ�1����2���ļ��㣬�����������⣺
��ͼ�ۡ�BAD=90������BAC=��FAD= ![]() ��
��![]() ����ǣ�����һ��45��,45��,90��ֱ�����ǰ��һֱ�DZ���AD���غϣ���Ƕ���A���BAD�Ķ����غϣ�AE�ǡ�CAF�Ľ�ƽ����������ǣ������˵����������ǣ���˵�����ɣ�
����ǣ�����һ��45��,45��,90��ֱ�����ǰ��һֱ�DZ���AD���غϣ���Ƕ���A���BAD�Ķ����غϣ�AE�ǡ�CAF�Ľ�ƽ����������ǣ������˵����������ǣ���˵�����ɣ�

���𰸡�(1)15��,�ƽ�У�(2)����������3��������.
�������������������1����CAE=��BAD����BAC����EAD=15������ΪAB��AD��AB��BC��
����BC��AD�ƽ�У���2���ȼ������EAB��=��EAD����B��AC��=15�����ɣ�1���ɵá�EAB��=��CAE������AE�ǡ�CAB���Ľ�ƽ��������3���ֱ�������CAE=��FAE=45������������AE�ǡ�CAF�Ľ�ƽ���ߣ�
���������
��1����AB��AD��
���BAD=90����
���CAE=90����45����30��=15����
��AB��AD��AB��BC��
��BC��AD�ƽ�У�
��2��AE�ǡ�CAB���Ľ�ƽ���ߣ�
�������£���ͼ�����ߡ�EAD=45������B��AC��=30����
���EAB��=��EAD����B��AC��=15����
���ɣ�1��֪����CAE=15����
���CAE=��EAB������AE�ǡ�CAB���Ľ�ƽ���ߣ�
��3��AE�ǡ�CAF�Ľ�ƽ���ߣ�
�������£���ͼ�����ߡ�EAD=45������BAD=90����
���BAE=��DAE=45����
�֡ߡ�BAC=��FAD=����
���BAE����BAC=��DAE����FAD��
���CAE=��FAE����AE�ǡ�CAF�Ľ�ƽ���ߣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�