题目内容
【题目】如图所示，甲、乙、丙、丁四个长方形拼成正方形EFGH，中间阴影为正方形．已知甲、乙、丙、丁四个长方形面积的和是32cm2 ， 四边形ABCD的面积是20cm2 ， 则甲、乙、丙、丁四个长方形周长的总和为cm．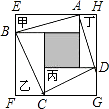 
【答案】48
【解析】解：∵阴影部分的面积=20﹣32÷2=4cm2∴S正方形EFGH=S阴影+S甲乙丙丁的面积和=4+32=36cm2
∴FG=6cm
∴正方形EFGH的周长=24cm
∴甲、乙、丙、丁四个长方形周长的总和=24×2=48cm．
所以答案是48．
【考点精析】解答此题的关键在于理解矩形的性质的相关知识，掌握矩形的四个角都是直角，矩形的对角线相等，以及对正方形的性质的理解，了解正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．
练习册系列答案
相关题目
