题目内容
【题目】用棋子按照一定规律摆放图形
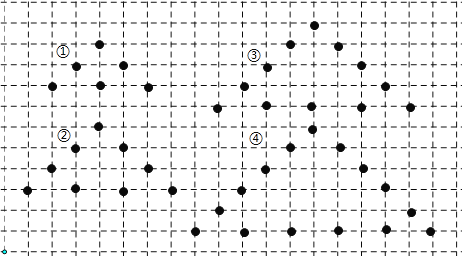
按照这种方式继续摆放下去,若摆放一个图形用去21枚棋子,则是摆放的第______个图形;摆放前n(n为正整数)个图形共需用______枚棋子.
【答案】⑥ ![]()
【解析】
设摆第n个图形需要an个棋子(n为正整数),根据图中棋子枚数的变化可得出“an=3(n+1)(n为正整数)”,代入an=21可求出用21枚棋子摆的图形的序号,再将前n个图形所用棋子数相加即可得出结论.
设摆第n个图形需要an个棋子(n为正整数),
观察图形,可知:a1=3×3-3=6,a2=3×4-3=9,a3=3×5-3=12,a4=3×6-3=15,
∴an=3×(n+2)-3=3(n+1)(n为正整数).
当an=21时,3(n+1)=21,
解得:n=6,
∴若摆放一个图形用去21枚棋子,则是摆放的第⑥个图形.
∵6+9+12+…+3(n+1)=![]() =
=![]() ,
,
∴摆放前n(n为正整数)个图形共需用![]() 枚棋子.
枚棋子.
故答案为:⑥;![]() .
.

练习册系列答案
相关题目