题目内容
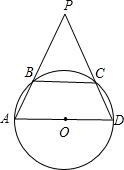如图，已知ABCD是一个以AD为直径的圆内接四边形，分别延长AB和DC，它们相交于P，若∠APD=60°，AB=5，PC=4，则⊙O的面积为（ ）| A、25π | B、16π | C、15π | D、13π |
分析：连接AC，由圆周角定理可得出∠ACD=90°，再由圆内接四边形的性质及三角形内角和定理可求出∠PAC=30°，由直角三角形的性质可求出AP、AC的长，由相似三角形的判定定理及性质可得出CD的长，再根据勾股定理接可求出AD的长，进而求出该圆的面积．
解答：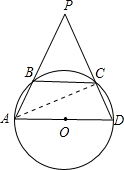
解：连接AC，
∵AD是⊙O的直径，
∴∠ACD=90°，
∵∠APD=60°，
∴∠PAC=30°，
∴AP=2PC=2×4=8，
∵AB=5，
∴PB=8-5=3，
∵四边形ABCD是以AD为直径的圆内接四边形，
∴∠BAD+∠BCD=180°，
∵∠BCD+∠PCB=180°，
∴∠BAD=∠PCB，∠APD=∠APD，
∴△PCB∽△PAD，
∴
=
，即
=
，PD=6，
∴CD=PD-PC=6-4=2，
∴AC=
=
=4
，
在Rt△ACD中，AD=
=
=2
．
∴OA=
AD=
，
∴⊙O的面积=π×（
）2=13π．
故选D．
解：连接AC，∵AD是⊙O的直径，
∴∠ACD=90°，
∵∠APD=60°，
∴∠PAC=30°，
∴AP=2PC=2×4=8，
∵AB=5，
∴PB=8-5=3，
∵四边形ABCD是以AD为直径的圆内接四边形，
∴∠BAD+∠BCD=180°，
∵∠BCD+∠PCB=180°，
∴∠BAD=∠PCB，∠APD=∠APD，
∴△PCB∽△PAD，
∴
| PC |
| AP |
| PB |
| PD |
| 4 |
| 8 |
| 3 |
| PD |
∴CD=PD-PC=6-4=2，
∴AC=
| AP2-PC2 |
| 82-42 |
| 3 |
在Rt△ACD中，AD=
| AC2+CD2 |
(4
|
| 13 |
∴OA=
| 1 |
| 2 |
| 13 |
∴⊙O的面积=π×（
| 13 |
故选D．
点评：本题考查的是相似三角形的判定与性质、圆内接四边形的性质、勾股定理，解答此题的关键是作出辅助线，构造出直角三角形求解．
练习册系列答案
相关题目
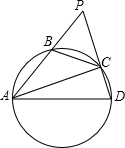如图，已知ABCD是一个半径为R的圆内接四边形，AB=12，CD=6，分别延长AB和DC，它们相交于点P，且BP=8，∠APD=60°，则R=
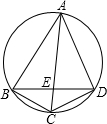如图，已知ABCD是圆的内接四边形，对角线AC和BD相交于E，BC=CD=4，AE=6，如果线段BE和DE的长都是整数，则BD的长等于
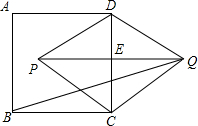如图，已知ABCD是正方形，以CD为一边向CD两旁作等边三角形PCD和等边三角形QCD，那么tan∠PQB的值为
如图，已知ABCD是圆O的内接四边形，AB=BD，BM⊥AC于M，求证：AM=DC+CM．