题目内容
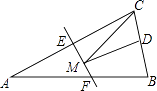
【题目】如图,AF是△ABC的高,AD是△ABC的角平分线,∠B=36°,∠C=76°,求∠DAF的度数. 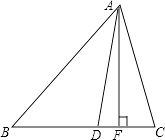
【答案】解:由三角形的外角性质知:∠ADF=∠B+ ![]() ∠BAC, 故∠B+
∠BAC, 故∠B+ ![]() ∠BAC+∠DAF=90°;①
∠BAC+∠DAF=90°;①
△ABC中,由三角形内角和定理得:
∠C+∠B+∠BAC=180°,
即: ![]() ∠C+
∠C+ ![]() ∠B+
∠B+ ![]() ∠BAC=90°,②
∠BAC=90°,②
②﹣①,得:
∠DAF= ![]() (∠C﹣∠B)=20°
(∠C﹣∠B)=20°
【解析】在△ADF中,由三角形的外角性质知:∠ADF=∠B+ ![]() ∠BAC,所以∠B+
∠BAC,所以∠B+ ![]() ∠BAC+∠FAD=90°,联立△ABC中,由三角形内角和定理得到的式子,即可推出∠DAF,∠B,∠C的关系,再代值求解即可.
∠BAC+∠FAD=90°,联立△ABC中,由三角形内角和定理得到的式子,即可推出∠DAF,∠B,∠C的关系,再代值求解即可.
【考点精析】本题主要考查了角的平分线和三角形的内角和外角的相关知识点,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题.

练习册系列答案
相关题目