题目内容
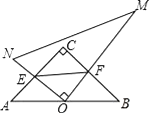
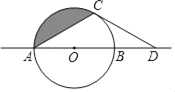
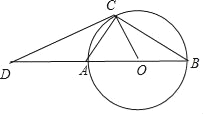
【题目】如图,⊙O半径为1,AB是⊙O的直径,C是⊙O上一点,连接AC,⊙O外的一点D 在直线AB上.
(1)若AC=![]() ,OB=BD.
,OB=BD.
①求证:CD是⊙O的切线.
②阴影部分的面积是 .(结果保留π)
(2)当点C在⊙O上运动时,若CD是⊙O的切线,探究∠CDO与∠OAC的数量关系.
【答案】(1)①见解析;②![]() ;(2)2∠OAC﹣∠ODC=90°或∠ODC+2∠OAC=90°
;(2)2∠OAC﹣∠ODC=90°或∠ODC+2∠OAC=90°
【解析】分析:![]() ①连接BC,OC,用勾股定理求出
①连接BC,OC,用勾股定理求出![]() 证明
证明![]() 为等边三角形,得到
为等边三角形,得到![]() 进而求出
进而求出![]() 得到
得到![]() 即可说明CD是
即可说明CD是![]() 切线.
切线.
②过C作![]() 于E,根据S阴=S扇形OAC﹣S△AOC,计算即可.
于E,根据S阴=S扇形OAC﹣S△AOC,计算即可.
![]() 分
分![]() 和
和![]() 两种情况进行讨论.
两种情况进行讨论.
详解:(1)①证明:连接BC,OC,
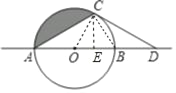
∵AB是直径,
∴![]()
在![]() 中:
中:![]()
∴![]()
∴![]() 为等边三角形,
为等边三角形,
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴CD是![]() 切线.
切线.
②过C作![]() 于E,
于E,
∵![]()
∴![]()
∴S阴=S扇形OAC﹣S△AOC,
![]()
![]()
故答案为:![]()
(2)①当![]() 时,
时,
∵CD是⊙O的切线,
∴![]()
![]()
∵![]()
∴![]()
![]()
即![]()
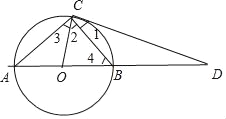
②当![]() 时,
时,
同①![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
综上:![]() 或
或![]()

练习册系列答案
相关题目