题目内容
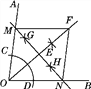
【题目】如图,在![]() ABCD中,E为对角线AC延长线上的一点.
ABCD中,E为对角线AC延长线上的一点.
(1)若四边形ABCD是菱形,求证:BE=DE.
(2)写出(1)的逆命题,并判断其是真命题还是假命题,若是真命题,给出证明;若是假命题,举出反例.

【答案】见解析
【解析】试题分析:(1)根据“菱形ABCD的对角线互相垂直平分”的性质推知OE是△BDE的边BD上的中垂线,结合角平分线的性质可知△DEB为等腰三角形;
(2)(1)的逆命题是“若BE=DE,则四边形ABCD是菱形”.根据平行四边形ABCD的对角线相互平分知OD=OB,结合角平分线的性质推知OE是BD的中垂线,即平行四边形ABCD的对角线互相垂直.
试题解析:(1)连接BD,交AC于点O,

∵四边形ABCD是菱形,
∴AC⊥BD,且BO=OD.
又∵E是AC延长线上的一点,
∴EO是△BDE的边BD的中垂线,∠DEB的角平分线,
∴△DEB是等腰三角形,
∴BE=DE;
(2)(1)的逆命题是“若BE=DE,则四边形ABCD是菱形”,
它是真命题,理由如下:
∵平行四边形ABCD,对角线AC、BD交于点O,
∴BO=OD.
又∵BE=DE
∴EO⊥BD,即AC⊥BD,
∴四边形ABCD是菱形。

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目