题目内容
【题目】(1)学校“圆周率”数学社团遇到这样一个题目:
如图1,在![]() 中,点
中,点![]() 在线段
在线段![]() 上,
上,![]() ,求
,求![]() 的长.
的长.
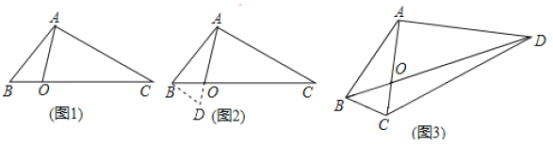
经过社团成员讨论发现,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,通过构造
,通过构造![]() 就可以解决问题(如图2). 请回答:
就可以解决问题(如图2). 请回答:![]() _______,
_______,![]() ______;
______;
(2)请参考以上解决思路,解决问题:
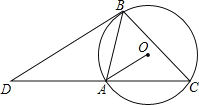
如图3,在四边形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长及四边形
的长及四边形![]() 的面积.
的面积.
【答案】(1)![]() ,10;(2)
,10;(2)![]() ,
,![]() .
.
【解析】
(1)根据平行线的性质可得出∠ADB=∠OAC=75°,结合∠BOD=∠COA可得出△BOD∽△COA,利用相似三角形的性质可求出OD的值,进而可得出AD的值,由三角形内角和定理可得出∠ABD=75°=∠ADB,由等角对等边可得出AB=AD=10,此题得解;(2)过点B作BE∥AD交AC于点E,同(1)可得出AE=10,在Rt△AEB中,利用勾股定理可求出BE的长度,再在Rt△CAD中,利用勾股定理可求出DC的长,此题得解;四边形ABCD的面积等于△ABC和△ADC的面积之和,利用以求的数据求解即可.
解:(1)∵BD∥AC,
∴∠ADB=∠OAC=75°.
∵∠BOD=∠COA,
∴△BOD∽△COA,
∴![]() .
.
又∵AO=8,
∴OD=![]() AO=2,
AO=2,
∴AD=AO+OD=10.
∵∠BAD=30°,∠ADB=75°,
∴∠ABD=180°-∠BAD-∠ADB=75°=∠ADB,
∴AB=AD=10.
故答案为:![]() ,10.
,10.
(2)过点B作BE∥AD交AC于点E,如图所示.
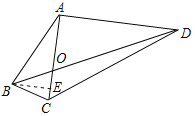
∵AC⊥AD,BE∥AD,
∴∠DAC=∠BEA=90°.
∵∠AOD=∠EOB,
∴△AOD∽△EOB,
∴![]()
∵BO:OD=1:4,
∴![]() .
.
∵AO=8,
∴EO=2,
∴AE=10.
∵∠ABC=∠ACB=75°,
∴∠BAC=30°,AB=AC,
又∵![]()
∴AB=2BE.
在Rt△AEB中,BE2+AE2=AB2,即102+BE2=(2BE)2,
解得:BE=![]() ,
,
∴AB=AC=![]() ,AD=
,AD=![]() .
.
在Rt△CAD中,AC2+AD2=CD2,
∴CD=![]() .
.
![]()
=![]() .
.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案【题目】暑假到了,即将迎来手机市场的销售旺季.某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
甲 | 乙 | |
进价(元/部) | 4000 | 2500 |
售价(元/部) | 4300 | 3000 |
该商场计划投入15.5万元资金,全部用于购进两种手机若干部,期望全部销售后可获毛利润不低于2万元.(毛利润=(售价﹣进价)×销售量)
(1)若商场要想尽可能多的购进甲种手机,应该安排怎样的进货方案购进甲乙两种手机?
(2)通过市场调研,该商场决定在甲种手机购进最多的方案上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.