Question

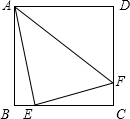如图，在正方形ABCD中，点E，F分别在边BC，CD上，如果AE=4，EF=3，AF=5，那么正方形ABCD的面积等于

 

．

Answer 1

分析：根据△ABE∽△ECF，可将AB与BE之间的关系式表示出来，在Rt△ABE中，根据勾股定理AB²+BE²=AC²，可将正方形ABCD的边长AB求出，进而可将正方形ABCD的面积求出．

解答：解：设正方形的边长为x，BE的长为a
∵∠AEB+∠BAE=∠AEB+∠CEF=90°
∴∠BAE=∠CEF
∵∠B=∠C
∴△ABE∽△ECF
∴

AB

CE

=

AE

EF

，即

x

x-a

=

4

3

解得x=4a①
在Rt△ABE中，AB²+BE²=AE²
∴x²+a²=4²②
将①代入②，可得：a=

4 17

17

∴正方形ABCD的面积为：x²=16a²=

256

17

．

点评：本题是一道根据三角形相似和勾股定理来求正方形的边长结合求解的综合题．隐含了整体的数学思想和正确运算的能力．注意后面可以直接这样x²+a²=4²②，∴x²+（

x

4

）²=4²，x²+

1

16

x²=4²，

17

16

x²=16，x²=

256

17

．无需算出算出x．