题目内容
【题目】已知二次函数y＝2x2＋4x－6．
(1)将其化成y＝a(x－h)2＋k的形式；
(2)写出开口方向，对称轴方程，顶点坐标；
(3)求图象与两坐标轴的交点坐标；
(4)画出函数图象；
(5)说明其图象与抛物线y＝x2的关系；
(6)当x取何值时，y随x增大而减小；
(7)当x取何值时，y＞0，y＝0，y＜0；
(8)当x取何值时，函数y有最值?其最值是多少?
(9)当y取何值时，－4＜x＜0；
(10)求函数图象与两坐标轴交点所围成的三角形面积．
【答案】(1)y＝2(x＋1)2－8；
(2)开口向上，直线x＝－1，顶点(－1，－8)；
(3)与x轴交点(－3，0)(1，0)，与y轴交点(0，－6)；
(4)图略；
(5)将抛物线y＝x2向左平移1个单位，向下平移8个单位；然后图像上所有点横坐标扩大为原来的2倍，得到y＝2x2＋4x－6的图象；
(6)x≤－1；
(7)当x＜－3或x＞1时，y＞0；当x＝－3或x＝1时，y＝0；
当－3＜x＜1时，y＜0；
(8)x＝－1时，y最小值＝－8；
(9)－8≤y＜10；
(10)S△＝12．
【解析】试题分析：（1）将函数表达式配方成顶点式形式，先将二次项、一次项分别提取a，然后加上
，再减去
即可得到y＝2(x＋1)2－8.（2）由a值的正负，或图像可判断开口方向。顶点式可看出对称轴和顶点坐标。（3）分别让x=0,y=0可分别求出图像与y轴的坐标，和x轴的坐标.（4）可根据顶点坐标，图像与x、y轴交点坐标，简略画出函数图像.（5）将抛物线y＝x2经过一定的平移可得到y＝2(x＋1)2－8.（6）根据函数图像可判断函数的增减性，最值以及x的取值与y.
试题解析：（1）通过配方法可以将y＝2x2＋4x－6配方成y＝2(x＋1)2－8.
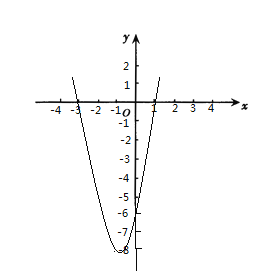
（2）由图像可以看出开口向上，由顶点式得对称轴为直线x＝－1，顶点坐标为(－1，－8)；
(3)当y=0时求得与x轴交点(－3，0)(1，0)，可求得当x=0时与y轴交点(0，－6)；
（4）如图所示为抛物线图像；（5）函数图像与抛物线y＝x2的关系：观察图可知，是由抛物线y＝x2先向左平移一个单位，然后图像上所有点横坐标扩大为原来的2倍，然后再向下平移八个单位得到的；（6）观察图，在对称轴左边，即x≤-1时，y随x的增大而减小。（7）有图得，x<-3或x>1时，y>0；当x=-3或x=1时，y=0；当-3<x<1时，y<0;（8）由图得，当x=-1时，y有最小值，y最小=-8；（9）当x=-4时，y=10;当x=0时，y=-8；所以，当-8≤y≤10时，-4≤x≤0；（10）函数图像与坐标轴交点坐标分别为（-3,0）、（1,0）、（0，-6），所以围成的三角形面积S=（3+1）×6×
=12.
