题目内容
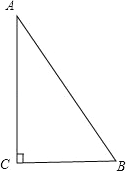
【题目】在△ABC，∠C=90°，斜边AB=10，直角边AC、BC的长是关于x的方程x2﹣mx+3m+6=0的两个实数根．
（1）求m的值；
（2）计算sinA+sinB+sinAsinB．
【答案】（1）m=14；（2）
【解析】
试题分析：（1）Rt△ABC中，AB2=AC2+BC2=（AC+BC）2﹣2AC×BC，再将二次方程的系数代入求得m值；
（2）将sinA+sinB+sinAsinB用△ABC的边表示，化为两边之和，两边之积，将二次方程的系数代入求得结果．
解：（1）如图，设AC=x1，BC=x2，
由题意，得
x1+x2=m＞0，x1x2=3m+6＞0．
在Rt△ABC中，AC2+BC2=100，
即x12+x22=100，
（x1+x2）2﹣2x1x2=100．
m2﹣6m﹣112=0．
解得m1=14，m2=﹣8（舍去）．
∴m=14．
（2）sinA+sinB+sinAsinB=
=
由x1+x2=m=14，x1x2=3m+6=3×14+6=48得：
=
．
练习册系列答案
相关题目
【题目】张华记录了今年雨季钱塘江一周内水位变化的情况如下表（正号表示比前一天高，负号表示比前一天低）：
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化（m） | +0.25 | +0.80 | ﹣0.40 | +0.03 | +0.28 | ﹣0.36 | ﹣0.04 |
（1）本周星期 水位最高，星期 水位最低．
（2）与上周末相比，本周日的水位是上升了还是下降了？（写出计算过程）
（2）请用折线统计图表示钱塘江一周内水位变化的情况．
