题目内容
 如图,等腰梯形ABCD中,AD∥BC,AB=DC,AC⊥BD,垂足为点O,过D点作DE∥AC交BC的延长线于点E.
如图,等腰梯形ABCD中,AD∥BC,AB=DC,AC⊥BD,垂足为点O,过D点作DE∥AC交BC的延长线于点E.
(1)求证:△BDE是等腰直角三角形;
(2)已知sin∠CDE=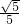 ,求AD:BE的值.
,求AD:BE的值.
(1)证明:∵AD∥BE,BE∥AC,
∴ACED是平行四边形,
∴AC=DE,
∵等腰梯形ABCD,
∴AC=BD,
∴BD=DE
∵AC⊥BD,
∴∠BOC=90°,
∵AC∥DE,
∴∠BOC=∠BDE=90°,
∴△BDE是等腰直角三角形.
(2)解:∵AD∥BC,
∴ ,
,
∴
∵等腰梯形ABCD,
∴AC=BD,
∴OC=OB,OA=OD,
∵AC∥DE,
∴∠CDE=∠DCO,
∴sin∠CDE=sin∠DCO=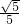 ,
,
在Rt△DCO中,设OD=k,DC= k (k>0),则OC=
k (k>0),则OC= =2k,
=2k,
∵平行四边形ACDE,
∴AD=CE,
∴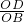 =
= =
= ,
,
∴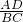 =
= ,
,
∴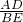 =
= .
.
分析:(1)推出平行四边形ACED,根据等腰梯形性质得出AC=DE=BD,得出等腰三角形,根据平行线性质求出∠BOC=∠BDE=90°,即可得出答案;
(2)根据平行线分线段成比例定理得出 ,根据等腰三角形性质得出AC=BD,推出OC=OB,OA=OD,根据平行线得出sin∠CDE=sin∠DCO=
,根据等腰三角形性质得出AC=BD,推出OC=OB,OA=OD,根据平行线得出sin∠CDE=sin∠DCO=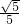 ,在Rt△DCO中,设OD=k,DC=
,在Rt△DCO中,设OD=k,DC= k 求出OC=2k,平行四边形的性质求出AD=CE,求出
k 求出OC=2k,平行四边形的性质求出AD=CE,求出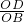 =
= ,求出
,求出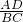 的值.即可求出答案.
的值.即可求出答案.
点评:本题考查了等腰梯形的性质,平行四边形的性质和判定,等腰三角形的判定,勾股定理、解直角三角形等知识点,主要考查学生综合运用性质进行推理和计算的能力,题目综合性比较强,有一定的难度.
∴ACED是平行四边形,
∴AC=DE,
∵等腰梯形ABCD,
∴AC=BD,
∴BD=DE
∵AC⊥BD,
∴∠BOC=90°,
∵AC∥DE,
∴∠BOC=∠BDE=90°,
∴△BDE是等腰直角三角形.
(2)解:∵AD∥BC,
∴
 ,
,∴

∵等腰梯形ABCD,
∴AC=BD,
∴OC=OB,OA=OD,
∵AC∥DE,
∴∠CDE=∠DCO,
∴sin∠CDE=sin∠DCO=
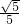 ,
,在Rt△DCO中,设OD=k,DC=
 k (k>0),则OC=
k (k>0),则OC= =2k,
=2k,∵平行四边形ACDE,
∴AD=CE,
∴
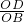 =
= =
= ,
,∴
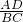 =
= ,
,∴
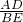 =
= .
.分析:(1)推出平行四边形ACED,根据等腰梯形性质得出AC=DE=BD,得出等腰三角形,根据平行线性质求出∠BOC=∠BDE=90°,即可得出答案;
(2)根据平行线分线段成比例定理得出
 ,根据等腰三角形性质得出AC=BD,推出OC=OB,OA=OD,根据平行线得出sin∠CDE=sin∠DCO=
,根据等腰三角形性质得出AC=BD,推出OC=OB,OA=OD,根据平行线得出sin∠CDE=sin∠DCO=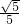 ,在Rt△DCO中,设OD=k,DC=
,在Rt△DCO中,设OD=k,DC= k 求出OC=2k,平行四边形的性质求出AD=CE,求出
k 求出OC=2k,平行四边形的性质求出AD=CE,求出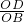 =
= ,求出
,求出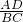 的值.即可求出答案.
的值.即可求出答案.点评:本题考查了等腰梯形的性质,平行四边形的性质和判定,等腰三角形的判定,勾股定理、解直角三角形等知识点,主要考查学生综合运用性质进行推理和计算的能力,题目综合性比较强,有一定的难度.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 14、如图,等腰梯形ABCD中,AB∥CD,∠A=60°,BD平分∠ABC,若梯形ABCD的周长为40cm,则CD的长为( )
14、如图,等腰梯形ABCD中,AB∥CD,∠A=60°,BD平分∠ABC,若梯形ABCD的周长为40cm,则CD的长为( )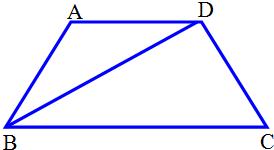 24、已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC.
24、已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC. (2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=
(2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD= 如图,等腰梯形ABCD中,AD∥BC,AB=CD,对角线BD平分∠ABC,且BD⊥DC,上底AD=3cm.
如图,等腰梯形ABCD中,AD∥BC,AB=CD,对角线BD平分∠ABC,且BD⊥DC,上底AD=3cm. 如图,等腰梯形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥DC,延长BC到E,使CE=AD.
如图,等腰梯形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥DC,延长BC到E,使CE=AD.