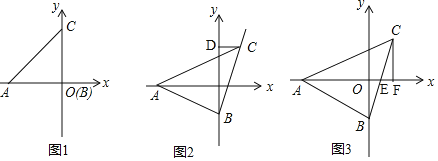
题目内容
【题目】已知,△ADB内接于⊙O,DG⊥AB于点G,交⊙O于点C,点E是⊙O上一点,连接AE分别交CD、BD于点H、F.
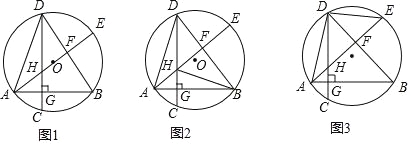
(1)如图1,当AE经过圆心O时,求证:∠AHG=∠ADB;
(2)如图2,当AE不经过点O时,连接BC、BH,若∠GBC=∠HBG时,求证:HF=EF;
(3)如图3,在(2)的条件下,连接DE,若AB=8,DH=6,求sin∠DAE的值.
【答案】见解析.
【解析】
试题分析:(1)如图1中,连接BE,由DG∥BE,推出∠AEB=∠AHG,由∠ADB=∠AEB,即可推出∠ADB=∠AHG.
(2)连接AC、DE,EB、AC、BC.只要证明HG=CG,∠EDB=∠CDB,根据等腰三角形三线合一即可证明.
(3)过点O作ON⊥DE,OM⊥AB垂足分别为N、M,连接OD、OE、OA、OB.只要证明△NOE≌△MBO,推出NE=OM=3,OB=![]() =5,在RT△OMB中,根据sin∠OBM=
=5,在RT△OMB中,根据sin∠OBM=![]() ,计算即可.
,计算即可.
试题解析:证明:(1)如图1中,连接BE,
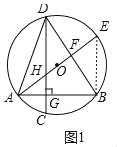
∵AE是⊙O的直径∴∠ABE=90°,
∵DG⊥AB,
∴∠ABE=∠AGD=90°,
∴DG∥BE,
∴∠AEB=∠AHG,
∵∠ADB=∠AEB
∴∠ADB=∠AHG.
(2)连接AC、DE,EB、AC、BC.
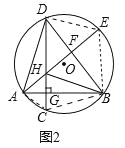
∠GBC=∠HBG,DG⊥AB
∴∠GHB=∠BCH,BH=BC,
∴HG=CG,
∴AH=AC,∠AHC=∠HCA,∠BAC=∠HAG
∵∠AED=∠ACH,∠DHE=∠AHC,
∴∠AED=∠DHE,
∴DH=DE,
∵∠EDB=∠EAB,∠CDB=∠BAC,
∴∠EDB=∠CDB,
∴HF=EF.
(3)过点O作ON⊥DE,OM⊥AB垂足分别为N、M,连接OD、OE、OA、OB.
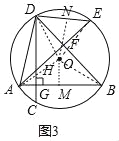
∴BM=![]() AB=4,
AB=4,
∵DH=DE=6,HF=EF,
∴DF⊥AE,
∴∠DAE+∠BDA=90°,
∵∠E O D=2∠DAE∠AO B=2∠ADB,
∴∠BOA+∠EOD=180°,
∵∠DOE=2∠NOE∠AOB=2∠BOM,
∴∠NOE+∠BOM=90°∠NOE+∠NEO=90°,
∵∠NEO=∠BOM,OE=OB,
∴△NOE≌△MBO
∴NE=OM=3,
∴OB=![]() =5,
=5,
∵∠ADB=∠BOM,
∴∠DAF=∠OBM,
在RT△OMB中sin∠OBM=![]() =
=![]()
∴sin∠DAE=![]() .
.

【题目】甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:
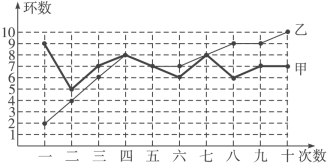
(1)请填写下表:
平均数 | 方差 | 中位数 | 命中9环及以上的次数 | |
甲 | 7 | 1.2 | 1 | |
乙 | 5.4 |
(2)请从下列四个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看;
②从平均数和中位数相结合看(分析谁的成绩好些);
③从平均数和命中9环以上的次数相结合看(分析谁的成绩好些);
④从折线图上两人射击命中环数的走势看(分析谁更有潜力).