��Ŀ����
����Ŀ����ͼ1��P��m��n����������y=![]() -1������һ�㣬l�ǹ�����0��-2������x��ƽ�е�ֱ�ߣ�����P��ֱ��PH��l������ΪH��
-1������һ�㣬l�ǹ�����0��-2������x��ƽ�е�ֱ�ߣ�����P��ֱ��PH��l������ΪH��
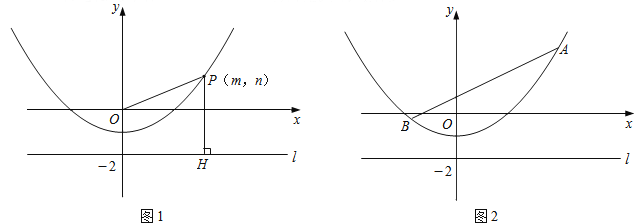
��̽����
��1����գ���m=0ʱ��OP= ��PH= ����m=4ʱ��OP= ��PH= ��
��֤����
��2��������m��n������OP��PH�Ĵ�С��ϵ����֤����IJ�����
��Ӧ�á�
��3����ͼ2����֪�߶�AB=6���˵�A��B��������y=![]() -1�ϻ�������A��B���㵽ֱ��l�ľ���֮�͵���Сֵ��
-1�ϻ�������A��B���㵽ֱ��l�ľ���֮�͵���Сֵ��
���𰸡���1��OP=1��PH=1��OP=5��PH=5����2��OP=PH��֤������������3��6��
��������
������1��m��ΪP��ĺ�������m=0ʱ��ֱ�Ӵ���x=0����P��0��-1������OP��PH����֪����m=4ʱ��ֱ�Ӵ���x=4����P��4��3����OP���й��ɶ�����ã�PH=yP-��-2����
��2������OP=PH��֤��ʱ��ΪPΪ����������κ���y=![]() -1�ĵ㣬һ�������m��
-1�ĵ㣬һ�������m��![]() -1����������1�����ù��ɶ�����PH=yP-��-2�������OP��PH���Ƚϼ��ý�����
-1����������1�����ù��ɶ�����PH=yP-��-2�������OP��PH���Ƚϼ��ý�����
��3��������2�����ۣ�������y=![]() -1�ĵ㵽ԭ��ľ�������䵽l�ľ�����Ҫ��A��B���㵽l����ĺͣ���A��B���㵽ԭ��ĺͣ���AB������O����OA+OB��AB=6����AB����O����OA+OB=AB=6������OA+OB��6����A��B���㵽l����ĺ͡�6��������Сֵ��Ϊ6��
-1�ĵ㵽ԭ��ľ�������䵽l�ľ�����Ҫ��A��B���㵽l����ĺͣ���A��B���㵽ԭ��ĺͣ���AB������O����OA+OB��AB=6����AB����O����OA+OB=AB=6������OA+OB��6����A��B���㵽l����ĺ͡�6��������Сֵ��Ϊ6��
�����������1���⣺OP=1��PH=1��OP=5��PH=5��
��ͼ1����PH��x�ύ��ΪQ��
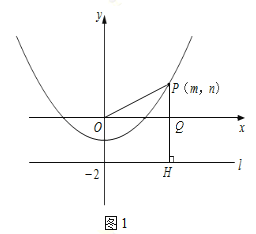
��m=0ʱ��P��0��-1������ʱOP=1��PH=1��
��m=4ʱ��P��4��3������ʱPQ=3��OQ=4��
��OP=![]() =5��PH=yP-��-2��=3-��-2��=5��
=5��PH=yP-��-2��=3-��-2��=5��
��2�����룺OP=PH��
֤��������P��PQ��x����Q��
��P�ڶ��κ���y=![]() -1�ϣ�
-1�ϣ�
����P��m��![]() -1������PQ=|
-1������PQ=|![]() -1|��OQ=|m|��
-1|��OQ=|m|��
�ߡ�OPQΪֱ�������Σ�
��OP=![]() ��
��
PH=yP-��-2��=��![]() -1��-��-2��=
-1��-��-2��=![]() ��
��
��OP=PH��
��3���⣺��ͼ2������OA��OB������A��AC��l��C������B��BD��l��D����ʱAC��ΪA�㵽l�ľ��룬BD��ΪB�㵽l�ľ�����
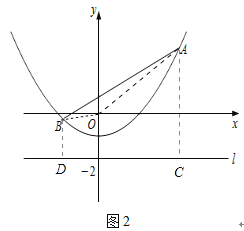
����AB����O��ʱ������OA��OB��
����OAB��OA+OB��AB=6��
���������۵ã�AC=OA��BD=OB��
��AC+BD��6��
����AB��O��ʱ��AC+BD=OA+OB=AB=6��
����AC+BD����СֵΪ6��
��A��B���㵽ֱ��l�ľ���֮�͵���СֵΪ6��