Question

【题目】定义：长宽比为：1（n为正整数）的矩形称为矩形．

下面，我们通过折叠的方式折出一个矩形，如图a所示．

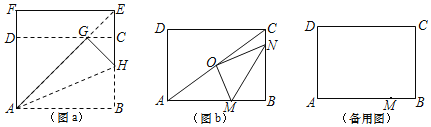
操作1：将正方形ABEF沿过点A的直线折叠，使折叠后的点B落在对角线AE上的点G处，折痕为AH．

操作2：将FE沿过点G的直线折叠，使点F、点E分别落在边AF，BE上，折痕为CD．则四边形ABCD为矩形．

（1）证明：四边形ABCD为矩形；

（2）点M是边AB上一动点．

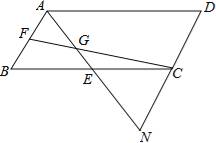
①如图b，O是对角线AC的中点，若点N在边BC上，OM⊥ON，连接MN．求tan∠OMN的值；

②若AM=AD，点N在边BC上，当△DMN的周长最小时，求的值；

③连接CM，作BR⊥CM，垂足为R．若AB=2，则DR的最小值= ．

Answer 1

【答案】（1）见解析；（2），2.

【解析】

（1）先判断出∠DAG=45°，进而判断出四边形ABCD是矩形，再求出AB：AD的值，即可得出结论；

（2）①如图b，先判断出四边形BQOP是矩形，进而得出，再判断出Rt△QON∽Rt△POM，进而判断出，即可得出结论；

②作M关于直线BC对称的点P，则△DMN的周长最小，判断出，得出AB=CD=a．进而得出BP=BM=AB-AM=（-1）a．即可得出结论；

③先求出BC=AD=2，再判断出点R是BC为直径的圆上，即可得出结论．

证明：（1）设正方形ABEF的边长为a，

∵AE是正方形ABEF的对角线，

∴∠DAG=45°，

由折叠性质可知AG=AB=a，∠FDC=∠ADC=90°，

则四边形ABCD为矩形，

∴△ADG是等腰直角三角形．

∴，

∴．

∴四边形ABCD为矩形；

（2）①解：如图，作OP⊥AB，OQ⊥BC，垂足分别为P，Q．

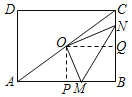
∵四边形ABCD是矩形，∠B=90°，

∴四边形BQOP是矩形．

∴∠POQ=90°，OP∥BC，OQ∥AB．

∴．

∵O为AC中点，

∴OP=BC，OQ=AB．

∵∠MON=90°，

∴∠QON=∠POM．

∴Rt△QON∽Rt△POM．

∴．

∴．

②解：如图c，作M关于直线BC对称的点P，连接DP交BC于点N，连接MN．则△DMN的周长最小，

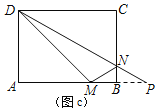
∵DC∥AP，

∴，

设AM=AD=a，则AB=CD=a．

∴BP=BM=AB-AM=（-1）a．

∴，

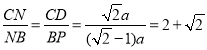③如备用图，

∵四边形ABCD为矩形，AB=2，

∴BC=AD=2，

∵BR⊥CM，

∴点R在以BC为直径的圆上，记BC的中点为I，

∴CI=BC=1，

∴DR最小=-1=2

故答案为：2