题目内容
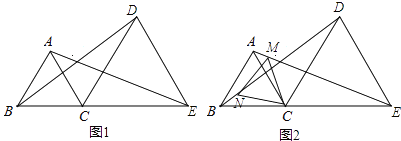
【题目】直线AB、CD相交于点O.
(1)OE、OF分别是∠AOC、∠BOD的平分线.画出这个图形.
(2)射线OE、OF在同一条直线上吗?(直接写出结论)
(3)画∠AOD的平分线OG.OE与OG有什么位置关系?并说明理由.
【答案】
(1)解:如图中红线所示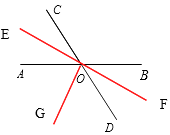
(2)解:∵ OE平分∠AOC ,OF平分∠BOD ,
∴ ∠COE=![]() ∠AOC ,∠DOF=
∠AOC ,∠DOF=![]() ∠BOD ,
∠BOD ,
∵ ∠AOC=∠BOD ,
∴ ∠EOC=∠DOF
,∵ ∠COE+∠EOD=180° ,
∴ ∠EOD+∠DOF=180° ,
即射线OE、OF在同一条直线上 。
(3)解:∵EF平分∠AOC和∠BOD,并且∠AOC=∠BOD,∴∠AOE=∠DOF.∵OG平分∠AOD,∴∠AOG=∠DOG.∵∠AOE+∠DOF+∠AOG+∠DOG=180°,∴∠DOF+∠DOG=180°÷2=90°,∴OE⊥OG
【解析】(1),用圆规在OA、OC上分别截取相等的线段,以与两边的交点为圆心,以大于![]() 交点间的距离的长为半径作弧,两弧在∠AOC内交于点E,作射线OE,则OE就是∠AOC的平分线,同理作出∠BOD的平分线;
交点间的距离的长为半径作弧,两弧在∠AOC内交于点E,作射线OE,则OE就是∠AOC的平分线,同理作出∠BOD的平分线;
(2),要判断射线OE,OF是否在同一直线上,只需判断∠EOD+∠DOF=180°是否成立,根据角平分线的性质可得 ∠COE=![]() ∠AOC ,∠DOF=
∠AOC ,∠DOF=![]() ∠BOD ,
∠BOD ,
再结合对顶角相等得, ∠EOC=∠DOF ,根据平角的定义得∠COE+∠EOD=180° , 从而得出 ∠EOD+∠DOF=180° ,即射线OE、OF在同一条直线上 ;
(3),根据角平分线的定义及对顶角相等得出∠AOE=∠DOF ,∠AOG=∠DOG ,根据平角的定义得出∠AOE+∠DOF+∠AOG+∠DOG=180° ,从而得出∠DOF+∠DOG=180°÷2=90°,即OE⊥OG 。

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案【题目】为响应市教育局倡导的“阳光体育运动”的号召,全校学生积极参与体育运动.为了进一步了解学校九年级学生的身体素质情况,体育老师在九年级800名学生中随机抽取50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如下所示:
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | a |
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
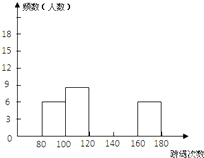
请结合图表完成下列问题:
(1)表中的a=;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第组;
(4)若九年级学生一分钟跳绳次数(x)达标要求是:x<120为不合格;120≤x<140为合格;140≤x<160为良;x≥160为优.根据以上信息,请你估算学校九年级同学一分钟跳绳次数为优的人数为 .