题目内容
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]()
(1)当![]() 时,求抛物线
时,求抛物线![]() 的顶点坐标;
的顶点坐标;
(2)已知点![]() ,抛物线
,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() (不与
(不与![]() 重合),将点
重合),将点![]() 绕点
绕点![]() 逆时针旋转90°至点
逆时针旋转90°至点![]() ,
,
①直接写出点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示);
的代数式表示);
②若抛物线![]() 与线段
与线段![]() 有且仅有一个公共点,求
有且仅有一个公共点,求![]() 的取值范围.
的取值范围.
【答案】(1)(3,2);(2)①(5-2a,2);②-1<a<![]() 或a=-2或a=-10
或a=-2或a=-10
【解析】
(1)将a代入抛物线,用配方法求顶点;
(2)①存在3种情况,具体情况见分析.逆时针旋转后,AC之间的距离即为点B横坐标的绝对值,纵坐标为2;
(2)②依旧按照2种情况分析,当2a-3>2时,画图发现,一定无交点;当2a-3<2时,首先可以确定抛物线过定点(1,-2)和(2,1),且点C在点A的下方,然后在用数形结合的方法,再细分为抛物线开口向上和开口向下的情况求解
(1)将a=-2代入抛物线得:![]()
配方得:![]()
∴顶点坐标为(3,2)
(2)①∵点C是抛物线与y轴的交点
∴当x=0时,y=2a-3
∴点C(0,2a-3)
分为2种情况进行讨论:
情况一:2a-3>2;
情况二:0<2a-3<2;
情况三:2a-3<0;
分析情况一,逆时针旋转90°图形如下:
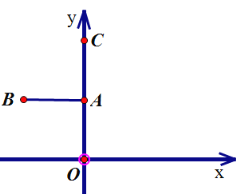
AC=2a-3-2=2a-5,∴AB=AC=2a-5
∴点B的横坐标为:-(2a-5)=5-2a,纵坐标为:2
∴B(5-2a,2)
情况二、三同理,也得到B(5-2a,2)
∴B(5-2a,2)
②抛物线的对称轴为:![]()
情况一:当2a-3>2,即a>![]() 时
时
点C在点A的上方,抛物线的开口向上,对称轴在y轴右侧,草图如下:
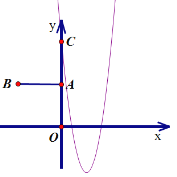
则抛物线与线段AB一定无交点
情况二:当2a-3<2,即a<![]() 时
时
∵抛物线![]()
化简得:![]()
故抛物线过定点:(1,-2),(2,1)
在求解过程中,还需要讨论抛物线的开口,需要继续细分:
第一种情况:当抛物线开口向下,a+1<0,即a<-1时,图形如下
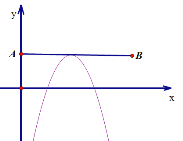
抛物线过定点(1,-2),(2,1),且开口向下,与线段AB仅有一个交点,则抛物线一定如上图所示,即定点在AB线段上,即定点的纵坐标为2
根据抛物线解析式,定点纵坐标为: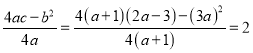
化简得:(a+2)(a+10)=0,解得:a=-2或a=-10
第二种情况,抛物线开口向上,a+1>0,即a>-1,且a<![]() ,即:-1<a<
,即:-1<a<![]() 时,图形如下:
时,图形如下:
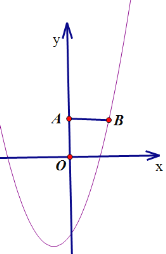
抛物线过定点(1,-2),(2,1),且开口向上,与线段AB仅有一个交点,则抛物线一定如上图所示(临界点),即当抛物线的右侧刚好经过点B时为临界点
∵B(5-2a,2)
∴只需当x=5-2a时,y>2即可
即:![]()
化简得:![]()
解得:-1<a<![]() 或a>
或a>![]() (舍)
(舍)
综合得:1<a<![]() 或a=-2或a=-10
或a=-2或a=-10