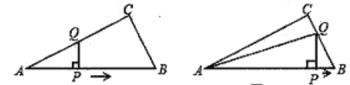题目内容
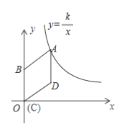
【题目】如图,在平面直角坐标系中,菱形![]() 的顶点
的顶点![]() 与原点
与原点![]() 重合,点
重合,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在反比例函数
在反比例函数![]() 的图象上,点
的图象上,点![]() 的坐标为
的坐标为![]() .
.
(1)求![]() 的值;
的值;
(2)若将菱形![]() 沿
沿![]() 轴正方向平移,当菱形的另一个顶点恰好落在函数
轴正方向平移,当菱形的另一个顶点恰好落在函数![]() 的图象上时,求菱形
的图象上时,求菱形![]() 平移的距离.
平移的距离.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)根据勾股定理求出OD的长度,再结合菱形的性质定理可得A点坐标,由此可求k的值;
(2)B和D可能落在反比例函数的图象上,分两种情况讨论,根据平移后纵坐标不变,求得平移后点的横坐标,由此可求得平移后的距离.
解:(1)过点![]() 作
作![]() 于点
于点![]() ,
,![]() 轴于点
轴于点![]() ,
,
∵点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
∴![]() .
.
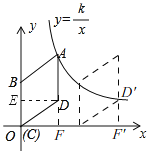
(2)由(1)可知反比例函数的解析式为![]() ,
,
将菱形![]() 沿
沿![]() 轴正方向平移,
轴正方向平移,
①若使点![]() 落在反比例函数
落在反比例函数![]() 的图象上的点
的图象上的点![]() 处,
处,
∴![]() ,
,
∴![]() 点的纵坐标为2,
点的纵坐标为2,
设点![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]() ,
,
∴菱形![]() 平移的距离为
平移的距离为![]() ;
;
②同理,若使点![]() 落在反比例函数
落在反比例函数![]() 的图象上,对应点
的图象上,对应点![]() 的纵坐标为3,
的纵坐标为3,
此时该点横坐标为:![]()
所以,菱形![]() 平移的距离为
平移的距离为![]() ,
,
综上,菱形![]() 平移的距离为
平移的距离为![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某超市随机选取1000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.假定每位顾客购买商品的可能性相同.
商品 顾客人数 | 甲 | 乙 | 丙 | 丁 |
100 | √ | × | √ | √ |
217 | × | √ | × | √ |
200 | √ | √ | √ | × |
300 | √ | × | √ | × |
85 | √ | × | × | × |
98 | × | √ | × | × |
(1)估计顾客同时购买乙和丙的概率为__________.
(2)如果顾客购买了甲,并且同时也在乙、丙、丁中进行了选购,则购买__________(填乙、丙、丁)商品的可能性最大.