��Ŀ����
����Ŀ����ͼ��������![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ���ڵ�
���ڵ�![]() ����֪������
����֪������![]() ��ֱ�ߵı���ʽΪ
��ֱ�ߵı���ʽΪ![]() ��
��
��1���������ߵĺ�������ʽ���䶥��![]() �����ꣻ
�����ꣻ
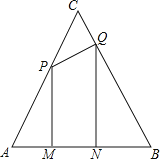
��2����ͼ������![]() ���߶�
���߶�![]() �ϵ�һ�����㣬����
�ϵ�һ�����㣬����![]() ����ֱ��
����ֱ��![]() �ᣬ��ֱ��
�ᣬ��ֱ��![]() ��
��![]() ������������
������������![]() ����
����![]() ��
��![]() �ᣬ��ֱ��
�ᣬ��ֱ��![]() �ڵ�
�ڵ�![]() ���ı���
���ı���![]() Ϊ���Σ������
Ϊ���Σ������![]() ���ܳ�Ϊ
���ܳ�Ϊ![]() ��д��
���![]() ��
��![]() �ĺ�����ϵʽ������
�ĺ�����ϵʽ������![]() Ϊ��ֵʱ�ܳ�
Ϊ��ֵʱ�ܳ�![]() ���
���
��3����ͼ�����������ߵĶԳ������Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() ���ɵ�����������
���ɵ�����������![]() Ϊ���ĵ��������Σ������ڣ�ֱ��д�����з��������ĵ�
Ϊ���ĵ��������Σ������ڣ�ֱ��д�����з��������ĵ�![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
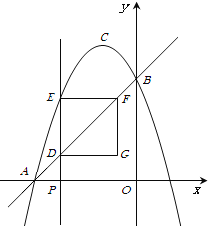
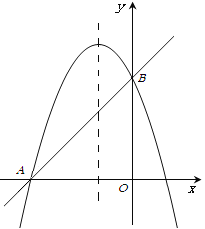
ͼ�� ͼ��
���𰸡���1�������ߵı���ʽΪy=-x2-2x+3������C����Ϊ��-1,4����
��2��L=-4m2-12m=-4��m+![]() ��2+9��
��2+9��
��m=-![]() ʱ�����ֵL=9��
ʱ�����ֵL=9��
��3����Q��������-1��![]() ������-1��-
������-1��-![]() ������-1��3+
������-1��3+![]() ������-1��3-
������-1��3-![]() ����
����
��������
���⣨1����ֱ�߾���A��B������������������꣬Ȼ�������κ�������ʽ�������b��c��ֵ���Ӷ��õ�����ʽ�������õ���������ꣻ
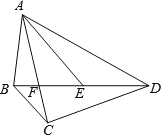
��2��������ɱ�ʾ��D��E�����꣬�Ӷ��õ�DE�ij�������֪�����ɵ�DE=EF���Ӷ��ɱ�ʾ������DEFG���ܳ�L�����ö��κ��������ʿ�������ֵ��
��3���ֱ��Ե�A����BΪԲ�ģ���AB��Ϊ�뾶��Բ��Բ��Գ���Ľ��㼴Ϊ����ĵ㣮
�����������1��ֱ��y=x+3��x���ཻ��A��-3,0 ������y���ཻ��B��0,3��
������y=-x2+bx+c����A��-3,0 ����B��0,3�������ԣ�
![]() ,
,
��![]() ��
��
���������ߵı���ʽΪy=-x2-2x+3��
��y=-x2-2x+3=-��x+1��2+4,
���ԣ���������ΪC��-1,4����
��2����ΪD��ֱ��y=x+3�ϣ���D��m,m+3����
��ΪE���������ϣ���E��m��-m2-2m+3����
DE=-m2-2m+3-��m+3��=-m2-3m��
�������֪��AO=BO,
���DAP=��ADP=��EDF=��EFD=45����
��DE=EF��
L=4DE=-4m2-12m��
L=-4m2-12m=-4��m+![]() ��2+9��
��2+9��
��a=-4<0,
�����κ��������ֵ
��m=-![]() ʱ�����ֵL=9��
ʱ�����ֵL=9��
��3����Q��������-1��![]() ������-1��-
������-1��-![]() ������-1��3+
������-1��3+![]() ������-1��3-
������-1��3-![]() ����
����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�