题目内容
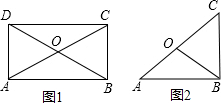 如图1所示,矩形ABCD的对角线AC、BD交于点O.
如图1所示,矩形ABCD的对角线AC、BD交于点O.(1)BO与对角线AC有怎样的数理关系.
(2)如果涂掉AD、OD、CD三条线段,如图2,这时,BO是Rt△ABC的斜边AC的什么线段?由(1)图能发现什么结论?试用语言描述.
分析:(1)根据矩形对角线相等且互相平分的性质,可得AC=BD且BO=DO,即可得BO=
AC;
(2)根据矩形对角线平分的性质可得AO=CO,即O为AC的中点,即BO=AO=CO.
| 1 |
| 2 |
(2)根据矩形对角线平分的性质可得AO=CO,即O为AC的中点,即BO=AO=CO.
解答:解:(1)∵矩形对角线相等且平分,
∴AC=BD,BO=DO,
故BO=
AC.
(2)BO是RT△ABC的斜边AC边上的中线.
由图(1)得BO=
AC,
语言描述:直角三角形斜边上的中线等于斜边的一半.
∴AC=BD,BO=DO,
故BO=
| 1 |
| 2 |
(2)BO是RT△ABC的斜边AC边上的中线.
由图(1)得BO=
| 1 |
| 2 |
语言描述:直角三角形斜边上的中线等于斜边的一半.
点评:本题考查了矩形对角线相等且平分的性质,考查了直角三角形中斜边中线等于斜边的一半的性质,本题中求得BO=
AC是解题的关键.
| 1 |
| 2 |

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
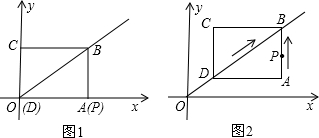
 出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值.
出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值.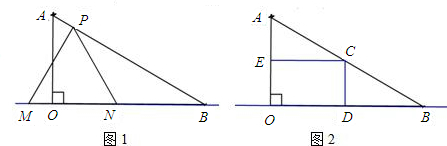

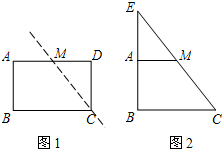 剪刀将形状如图1所示的矩形纸片ABCD沿着直线CM剪成两部分,其中M为AD的中点.用这两部分纸片可以拼成一些新图形,例如图2中的Rt△BCE就是拼成的一个图形.若利用这两部分纸片拼成的Rt△BCE是等腰直角三角形,设原矩形纸片中的边AB和BC的长分别为a厘米、b厘米,且a、b恰好是关于x的方程x2-(m-1)x+m+1=0的两个实数根,试求出原矩形纸片的面积.
剪刀将形状如图1所示的矩形纸片ABCD沿着直线CM剪成两部分,其中M为AD的中点.用这两部分纸片可以拼成一些新图形,例如图2中的Rt△BCE就是拼成的一个图形.若利用这两部分纸片拼成的Rt△BCE是等腰直角三角形,设原矩形纸片中的边AB和BC的长分别为a厘米、b厘米,且a、b恰好是关于x的方程x2-(m-1)x+m+1=0的两个实数根,试求出原矩形纸片的面积.