题目内容
如图1所示,矩形ABCD的两条边在坐标轴上,点D与原点重合,对角线BD所在直线的函数关系式为y=
x,AD=8.矩形ABCD沿DB方向以每秒1个单位长度运动,同时点P从点A出发做匀速运动,沿矩形ABCD的边经过点B到达点C,用了14秒.
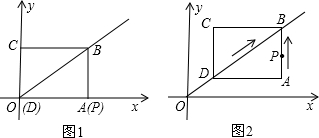
(1)求矩形ABCD的周长.
(2)如图2所示,图形运动到第5秒时,求点P的坐标.
(3)设矩形运动的时间为t,当0≤t≤6时,点P所经过的路线是一条线段,请求出线段所在直线的函数关系式.
(4)当点P在线段AB或BC上运动时,过点P作x轴、y轴的垂线,垂足分别为E、F,则矩形PEOF是否能与矩形ABCD相似(或位似)?若能,求出t的值;若不能,说明理由.
分析:(1)根据题意,AD=8,B点在y=
x上,则y=6,即B点坐标为(8,6),AB=6,可求得矩形的周长为28.
(2)由(1)可知AB+BC=14,点P的速度为每秒1个单位.可求得D点坐标为(4,3),点P坐标为(12,8);
(3)设线段所在直线为y=kx+b,把点(8,0),(12,8),代入解析式利用待定系数法求解得:函数关系式为y=2x-16;
(4)①当点P在AB边运动时,即0≤t≤6,点D的坐标表示为
(t,t),点P的坐标为(8+
t,
t),根据相似三角形的相似比,解得t=6;当点P与点B重合,此时矩形PEOF与矩形BADC是位似形.则根据相似三角形的相似比可解得t=20,因为20>6,所以此时点P不在AB边上,舍去.②当点P在BC边运动时,即6≤t≤14,则点D的坐标为
(t,t),点P的坐标为(14-
t,
t+6)
同样利用三角形的相似比可求得
t=,因为
>14,此时点P不在BC边上,舍去.
综合可知,当t=6时,点P到达点B,矩形PEOF与矩形BADC是位似形.
解答:解:(1)AD=8,B点在y=
x上,则y=6,B点坐标为(8,6),AB=6,矩形的周长为28.
(2)由(1)可知AB+BC=14,P点走过AB、BC的时间为14秒,因此点P的速度为每秒1个单位.
∵矩形沿DB方向以每秒1个单位长运动,出发5秒后,OD=5,此时D点坐标为(4,3),
同时点P沿AB方向运动了5个单位,则点P坐标为(12,8).
(3)点P运动前的位置为(8,0),5秒后运动到(12,8),
已知它运动路线是一条线段,设线段所在直线为y=kx+b
∴
,
解得:
函数关系式为y=2x-16.
(4)方法一:①当点P在AB边运动时,即0≤t≤6,
点D的坐标为
(t,t),
∴点P的坐标为(8+
t,
t).
若
=,则
=,解得t=6.
当t=6时,点P与点B重合,此时矩形PEOF与矩形BADC是位似形.
若
=,则
=,
解得t=20.
因为20>6,所以此时点P不在AB边上,舍去.
②当点P在BC边运动时,即6≤t≤14,
点D的坐标为
(t,t),
∴点P的坐标为(14-
t,
t+6).
若
=,则
=,
解得t=6.
因为
<14,此时点P不在BC边上,舍去.
综上,当t=6时,点P到达点B,矩形PEOF与矩形BADC是位似形.
方法二:当点P在AB上没有到达点B时,
<=,
更不能等于
.
则点P在AB上没到达点B时,两个矩形不能构成相似形
当点P到达点B时,矩形PEOF与矩形BADC是位似形,此时t=6.
当点P越过点B在BC上时,
>若
=时,由点P在BC上时,坐标为:
(14-
t,
t+6),(6≤t≤14),
=,
解得t=
,但
<14.
因此当P在BC上(不包括B点)时,矩形PEOF与矩形BCDA不相似.
综上,当t=6时,点P到达点B,矩形PEOF与矩形BADC是位似形.
点评:主要考查了函数和几何图形的综合运用.解题的关键是会灵活的运用函数图象的性质和交点的意义求出相应的线段的长度或表示线段的长度,再结合具体图形的性质求解.
练习册系列答案
相关题目


 通城学典默写能手系列答案
通城学典默写能手系列答案 出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值.
出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值.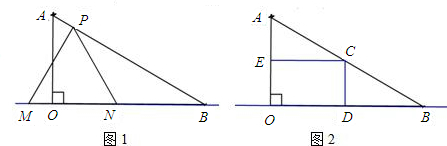

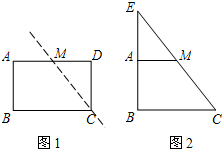 剪刀将形状如图1所示的矩形纸片ABCD沿着直线CM剪成两部分,其中M为AD的中点.用这两部分纸片可以拼成一些新图形,例如图2中的Rt△BCE就是拼成的一个图形.若利用这两部分纸片拼成的Rt△BCE是等腰直角三角形,设原矩形纸片中的边AB和BC的长分别为a厘米、b厘米,且a、b恰好是关于x的方程x2-(m-1)x+m+1=0的两个实数根,试求出原矩形纸片的面积.
剪刀将形状如图1所示的矩形纸片ABCD沿着直线CM剪成两部分,其中M为AD的中点.用这两部分纸片可以拼成一些新图形,例如图2中的Rt△BCE就是拼成的一个图形.若利用这两部分纸片拼成的Rt△BCE是等腰直角三角形,设原矩形纸片中的边AB和BC的长分别为a厘米、b厘米,且a、b恰好是关于x的方程x2-(m-1)x+m+1=0的两个实数根,试求出原矩形纸片的面积.