题目内容
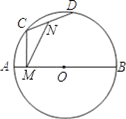
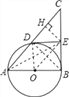
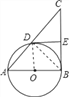
【题目】如图所示,以Rt△ABC的直角边AB为直径作圆O,与斜边交于点D,E为BC边上的中点,连接DE.
(1)求证:DE是⊙O的切线;
(2)连接OE,AE,当∠CAB为何值时,四边形AOED是平行四边形?并在此条件下求sin∠CAE的值.

【答案】(1)见解析;(2)![]() .
.
【解析】分析:(1)要证DE是⊙O的切线,必须证ED⊥OD,即∠EDB+∠ODB=90°
(2)要证AOED是平行四边形,则DE∥AB,D为AC中点,又BD⊥AC,所以△ABC为等腰直角三角形,所以∠CAB=45°,再由正弦的概念求解即可.
详解:(1)证明:连接O、D与B、D两点,
∵△BDC是Rt△,且E为BC中点,
∴∠EDB=∠EBD.(2分)
又∵OD=OB且∠EBD+∠DBO=90°,
∴∠EDB+∠ODB=90°.
∴DE是⊙O的切线.
(2)解:∵∠EDO=∠B=90°,
若要四边形AOED是平行四边形,则DE∥AB,D为AC中点,
又∵BD⊥AC,
∴△ABC为等腰直角三角形.
∴∠CAB=45°.
过E作EH⊥AC于H,
设BC=2k,则EH=![]() k,AE=
k,AE=![]() k,
k,
∴sin∠CAE=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目