题目内容
【题目】如图,在△ABC中,AB=AC,D为边BC的中点,以AB、BD为邻边作平行四边形ABDE,连接AD、EC。
求证:四边形ADCE是矩形。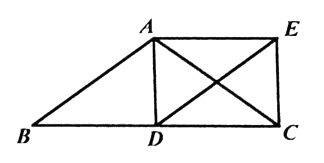
【答案】解:证明:∵AB=AC,D是BC的中点,
∴BD=CD,且AD⊥BC。
∵四边形ABDE是平行四边形,
∴AE=BD,AE//BD,
∴AE=CD,AE//CD,
∴四边形ADCE是平行四边形,
∵AD⊥CD,
∴□ABCD是矩形。
【解析】证四边形是矩形有两种思路,一是证有3个角是直角;二是先证它是平行四边形,再加一个矩形特有的性质条件即可。此题易得DE=BD=CD,且AE//BD,则四边形ADCE是平行四边形,又由AD⊥CD,即可证得。
【考点精析】通过灵活运用矩形的性质,掌握矩形的四个角都是直角,矩形的对角线相等即可以解答此题.

练习册系列答案
相关题目