题目内容
【题目】我县为了倡导居民节约用水,生活用水按阶梯式水价计费,如图是居民每户每月的水费y(元)与所用的水量x(吨)之间的函数图象,请根据图象所提供的信息,解答下列问题: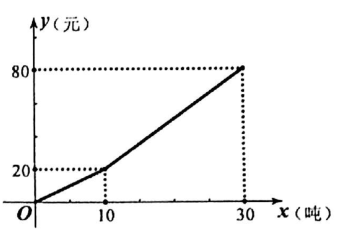
(1)当用水量不超过10吨时,每吨水收费多少元?
(2)当用水量超过10吨且不超过30吨时,求y与x之间的函数关系式;
(3)某户居民三、四月份水费共82元,四月份用水比三月份多4吨,求这户居民三月份用水多少吨。
【答案】
(1)
解:如图,当x=10时,水费是20元,则每吨水费为20÷10=2(元/吨)。
(2)
解:当10<x≤30时,设y=kx+b,将(10,20)和(30,80)代入可得
![]() 解得
解得 ![]()
∴直线y=3x-10(10<x≤30)。
(3)
解:设居民三月份用水x吨,则四月份用水x+4吨,
当x=10时,水费:2×10+3×14-10=52(元)<82元,
故x>10,则水费:3x-10+3(x+4)-10=82,解得x=15,
答:这户居民三月份用水15吨。
【解析】(1)根据图象可得,当0≤x≤10时,y是关于x的正比例函数,且x=10时,y=20,则可求得每吨的消费;(2)可设y=kx+b,经过(10,20)和(30,80),代入即可解得答案;(3)设居民三月份用水x吨,则四月份用水x+4吨,根据水费为82元,可分析x的取值范围,∵x=10是一个临界点,∴当x=10时,求出这时的水费与82比较,若结果大于82,表示x<10,若小于82,则表示x>10,然后构造方程求出x的值。
【考点精析】解答此题的关键在于理解一次函数的性质的相关知识,掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小.

练习册系列答案
相关题目