题目内容
【题目】在探究平行线的判定——基本事实：两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行时，老师布置了这样的任务：
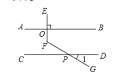
请同学们分组在学案上（如图），用直尺和三角尺画出过点P与直线AB平行的直线PQ；并思考直尺和三角尺在画图过程中所起的作用．
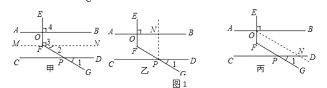
小菲和小明所在的小组是这样做的：他们选取直尺和含有45°角的三角尺，用平移三角尺的画图方法画出AB的平行线PQ，并将实际画图过程抽象出平面几何图形（如图）．
以下是小菲和小明所在小组关于直尺和三角尺作用的讨论：
①在画平行线的过程中，三角尺由初始位置靠着直尺平移到终止位置，实际上就是先画∠BMD=45°，再过点P画∠BMD=45°
②由初始位置的三角尺和终止位置的三角尺各边所在直线构成一个“三线八角图”，其中QP为截线
③初始位置的三角尺和终止位置的三角尺在“三线八角图”中构成一组同位角
④在画图过程中，直尺可以由直线CD代替
⑤在“三线八角图”中，因为AB和CD是截线，所以，可以下结论“两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行”
其中，正确的是（ ）
A.①②⑤B.①③④C.②④⑤D.③④⑤
【答案】B
【解析】
这种画法就是画同位角∠DMB和∠DEP相等，从而判断PQ∥AB，从而根据平行线的判定定理对各小题进行判断．
在画平行线的过程中，三角尺由初始位置靠着直尺平移到终止位置，实际上就是先画∠BMD=45°，再过点P画∠BMD=45°，所以①正确；
由初始位置的三角尺和终止位置的三角尺各边所在直线构成一个“三线八角图”，其中CD为截线，所以②错误；
初始位置的三角尺和终止位置的三角尺在“三线八角图”中构成一组同位角，所以③正确；
在画图过程中，直尺可以由直线CD代替，所以④正确；
⑤在“三线八角图”中，因为AB和PQ是一组平行线，CD为截线，所以，可以下结论“两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行”，所以⑤错误．
故选：B．
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
