��Ŀ����
����Ŀ����ͼ1����ABC�͡�CDE���ǵ���ֱ�������Σ���C=90�㣬����CDE�Ƶ�C��ʱ����תһ���ǶȦ���0�㣼����90�㣩��ʹ��A��D��E��ͬһֱ���ϣ�����AD��BE��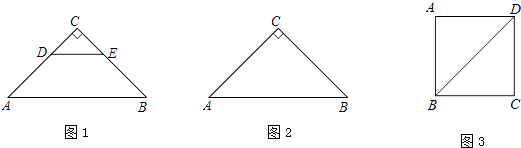
��1���������ⲹȫͼ2��
����֤��AD=BE����AD��BE��
����CM��DE������ΪM�����õ�ʽ��ʾ���߶�CM��AE��BE֮���������ϵ��
��2����ͼ3��������ABCD�߳�Ϊ ![]() ������P����PD=1���ҡ�BPD=90�㣬��ֱ��д����A��BP�ľ��룮
������P����PD=1���ҡ�BPD=90�㣬��ֱ��д����A��BP�ľ��룮
���𰸡�
��1��
�⣺���������ⲹȫͼ2������ͼ��һ����ʾ��

��֤�����ߡ�ACD+��DCB=��ACB=90�㣬��BCE+��DCB=��DCE=90�㣬
���ACD=��BCE��
�ߡ�ABC�͡�CDE���ǵ���ֱ�������Σ�
��AC=BC��DC=EC��
�ڡ�ADC�͡�BEC�У���  ��
��
���ADC�ա�BEC��SAS����
��AD=BE����BEC=��ADC��
�ߵ�A��D��E��ͬһֱ���ϣ���CDE�ǵ���ֱ�������Σ�
���CDE=��CED=45�㣬��ADC=180�㩁��CDE=135�㣬
���AEB=��BEC����CED=135�㩁45��=90�㣬
��AD��BE��
���������⻭��ͼ�Σ���ͼ��������ʾ��

��S��ABC+S��EBC=S��CAE+S��EAB��
�� ![]() ACBC+
ACBC+ ![]() BECM=
BECM= ![]() AE��CM+BE����
AE��CM+BE����
��AC2��AEBE=CM��AE��BE����
�ߡ�CDEΪ����ֱ�������Σ�
��DE=2CM��
��AE��BE=2CM
��2��
�⣺�������⻭��ͼ�Σ�������

����AB= ![]() ��DP=1��BD=
��DP=1��BD= ![]() AB=
AB= ![]()
�ɹ��ɶ����ã�BP= ![]() =3��
=3��
��ϣ�1���۵Ľ��ۿ�֪��
AM= ![]() =
= ![]() =1��
=1��
�ʵ�A��BP�ľ���Ϊ1
����������1���ٸ�����ת�����Ի���ͼ���ɡ�ACD����BCE�����DCB����ɵó���ACD=��BCE���ɡ�ABC�͡�CDE���ǵ���ֱ�������οɵó�AC=BC��DC=EC�����ȫ�������ε��ж�����SAS���ɵó���ADC�ա�BEC���Ӷ��ó�AD=BE�����ɡ�BCE=��ADC=135�㣬��CED=45�㼴�ɵó���AEB=90�㣬��֤��AD��BE�����������⻭��ͼ�Σ��������ͼ�ε����Ϊ���������ε�����Ϳ���AE��BEȥ��ʾCM����2���������⻭��ͼ�Σ����գ�1���۵Ľ��ۣ��������ݼ��ɵó����ۣ�
�����㾫����������Ĺؼ������������ֱ�������ε����֪ʶ�����յ���ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45�㣮

 �ǻ�С��ϰϵ�д�
�ǻ�С��ϰϵ�д�����Ŀ��������һ�����⣺̽������y= ![]() x2+
x2+ ![]() ��ͼ�������ʣ�
��ͼ�������ʣ�
С������ѧϰ�����ľ��飬�Ժ���y= ![]() x2+
x2+ ![]() ��ͼ�������ʽ�����̽����
��ͼ�������ʽ�����̽����
������С����̽�����̣��벹��������
��1������y= ![]() x2+
x2+ ![]() ���Ա���x��ȡֵ��Χ��
���Ա���x��ȡֵ��Χ��
��2���±���y��x�ļ����Ӧֵ��
x | �� | ��3 | ��2 | ��1 | �� | �� |
|
| 1 | 2 | 3 | �� |
y | �� |
|
| �� | �� | �� |
|
|
|
| m | �� |
��m��ֵ��
��3����ͼ����ƽ��ֱ������ϵxOy�У���������ϱ��и��Զ�ӦֵΪ����ĵ㣮��������ĵ㣬�����ú�����ͼ�� 
��4����һ��̽�����֣��ú���ͼ���ڵ�һ�����ڵ���͵�������ǣ�1�� ![]() ������Ϻ�����ͼ��д���ú������������ʣ�һ�����ɣ� ��
������Ϻ�����ͼ��д���ú������������ʣ�һ�����ɣ� ��





