ΧβΡΩΡΎ»ί
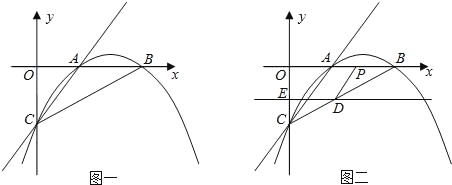
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ»γΆΦ“ΜΘ§≈ΉΈοœΏy=ax2+bx+c”κx÷α’ΐΑκ÷αΫΜ”ΎAΓΔBΝΫΒψΘ§”κy÷αΫΜ”ΎΒψCΘ§÷±œΏy=x-2Ψ≠ΙΐAΓΔCΝΫΒψΘ§«“AB=2Θ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
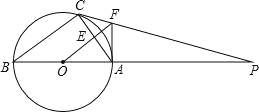
Θ®2Θ©»τ÷±œΏDEΤΫ––”Ύx÷α≤Δ¥”CΒψΩΣ Φ“‘ΟΩΟκ1ΗωΒΞΈΜΒΡΥΌΕ»―Ίy÷α’ΐΖΫœρΤΫ“ΤΘ§«“Ζ÷±πΫΜy÷αΓΔœΏΕΈBC”ΎΒψEΘ§DΘ§Ά§ ±Ε·ΒψP¥”ΒψB≥ωΖΔΘ§―ΊBOΖΫœρ“‘ΟΩΟκ2ΗωΒΞΈΜΥΌΕ»‘ΥΕ·Θ§Θ®»γΆΦ2Θ©ΘΜΒ±ΒψP‘ΥΕ·ΒΫ‘≠ΒψO ±Θ§÷±œΏDE”κΒψPΕΦΆΘ÷Ι‘ΥΕ·Θ§Ν§DPΘ§»τΒψP‘ΥΕ· ±ΦδΈΣtΟκΘΜ…ηs=![]() Θ§Β±tΈΣΚΈ÷Β ±Θ§s”–Ήν–Γ÷ΒΘ§≤Δ«σ≥ωΉν–Γ÷ΒΘ°
Θ§Β±tΈΣΚΈ÷Β ±Θ§s”–Ήν–Γ÷ΒΘ§≤Δ«σ≥ωΉν–Γ÷ΒΘ°
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§ «Ζώ¥φ‘ΎtΒΡ÷ΒΘ§ Ι“‘PΓΔBΓΔDΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςABCœύΥΤΘΜ»τ¥φ‘ΎΘ§«σtΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩ(1)y=-![]() x2+
x2+![]() x-2Θ°Θ®2Θ©Β±t=1 ±Θ§s”–Ήν–Γ÷ΒΘ§«“Ήν–Γ÷ΒΈΣ1Θ°Θ®3Θ©Β±t=
x-2Θ°Θ®2Θ©Β±t=1 ±Θ§s”–Ήν–Γ÷ΒΘ§«“Ήν–Γ÷ΒΈΣ1Θ°Θ®3Θ©Β±t=![]() Μρ
Μρ![]() ±Θ§“‘PΓΔBΓΔDΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςABCœύΥΤΘ°
±Θ§“‘PΓΔBΓΔDΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςABCœύΥΤΘ°
ΓΨΫβΈωΓΩ
‘ΧβΖ÷ΈωΘΚΘ®1Θ© Ήœ»ΗυΨί÷±œΏACΒΡΫβΈω Ϋ»ΖΕ®ΒψAΓΔCΒΡΉχ±ξΘ§“―÷ΣABΒΡ≥ΛΘ§Ϋχ“Μ≤ΫΡήΒΟΒΫΒψBΒΡΉχ±ξΘΜ»ΜΚσ”…¥ΐΕ®œΒ ΐΖ®»ΖΕ®≈ΉΈοœΏΒΡΫβΈω ΫΘ°
Θ®2Θ©ΗυΨίΥυΗχΒΡs±μ¥ο ΫΘ§“ΣΫβ¥πΗΟΧβΨΆ±Ί–κ÷ΣΒάEDΓΔOPΒΡ≥ΛΘΜBPΓΔCE≥Λ“Ή÷ΣΘ§Ρ«Ο¥”…OP=OB-BP«σΒΟOP≥ΛΘ§”…ΓœCEDΒΡ»ΐΫ«Κ· ΐ÷ΒΩ…ΒΟΒΫEDΒΡ≥ΛΘ§‘Ό¥ζ»κsΒΡ±μ¥ο Ϋ÷–Ω…ΒΟΒΫΙΊ”ΎsΓΔtΒΡΚ· ΐΙΊœΒ ΫΘ§ΫαΚœΚ· ΐΒΡ–‘÷ Φ¥Ω…ΒΟΒΫsΒΡΉν–Γ÷ΒΘ°
Θ®3Θ© Ήœ»«σ≥ωBPΓΔBDΒΡ≥ΛΘ§»τ“‘PΓΔBΓΔDΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςABCœύΥΤΘ§“―÷ΣΒΡΧθΦΰ «ΙΪΙ≤Ϋ«ΓœOBCΘ§Ρ«Ο¥±Ί–κ¬ζΉψΒΡΧθΦΰ «Φ–ΙΪΙ≤Ϋ«ΒΡΝΫΉιΕ‘”Π±Ώ≥…±»άΐΘ§Ζ÷ΝΫ÷÷«ιΩωΧ÷¬έΦ¥Ω…Θ°
‘ΧβΫβΈωΘΚΘ®1Θ©”…÷±œΏΘΚy=x-2÷ΣΘΚAΘ®2Θ§0Θ©ΓΔCΘ®0Θ§-2Θ©ΘΜ
ΓΏAB=2Θ§ΓύOB=OA+AB=4Θ§Φ¥BΘ®4Θ§0Θ©Θ°
…η≈ΉΈοœΏΒΡΫβΈω ΫΈΣΘΚy=aΘ®x-2Θ©Θ®x-4Θ©Θ§¥ζ»κCΘ®0Θ§-2Θ©Θ§ΒΟΘΚ
aΘ®0-2Θ©Θ®0-4Θ©=-2Θ§ΫβΒΟa=-![]()
Γύ≈ΉΈοœΏΒΡΫβΈω ΫΘΚy=-![]() Θ®x-2Θ©Θ®x-4Θ©=-
Θ®x-2Θ©Θ®x-4Θ©=-![]() x2+
x2+![]() x-2Θ°
x-2Θ°
Θ®2Θ©‘ΎRtΓςOBC÷–Θ§OB=4Θ§OC=2Θ§‘ρtanΓœOCB=2ΘΜ
ΓΏCE=tΘ§ΓύDE=2tΘΜ
ΕχOP=OB-BP=4-2tΘΜ
Γύs=![]() Θ®0ΘΦtΘΦ2Θ©Θ§
Θ®0ΘΦtΘΦ2Θ©Θ§
ΓύΒ±t=1 ±Θ§s”–Ήν–Γ÷ΒΘ§«“Ήν–Γ÷ΒΈΣ1Θ°
Θ®3Θ©‘ΎRtΓςOBC÷–Θ§OB=4Θ§OC=2Θ§‘ρBC=2![]() ΘΜ
ΘΜ
‘ΎRtΓςCED÷–Θ§CE=tΘ§ED=2tΘ§‘ρCD=![]() tΘΜ
tΘΜ
ΓύBD=BC-CD=2![]() -
-![]() tΘΜ
tΘΜ
“‘PΓΔBΓΔDΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςABCœύΥΤΘ§“―÷ΣΓœOBC=ΓœPBDΘ§‘ρ”–ΝΫ÷÷«ιΩωΘΚ
ΔΌ![]()
![]() Θ§ΫβΒΟt=
Θ§ΫβΒΟt=![]() ΘΜ
ΘΜ
ΔΎ![]()
![]() Θ§ΫβΒΟt=
Θ§ΫβΒΟt=![]() ΘΜ
ΘΜ
Ήέ…œΘ§Β±t=![]() Μρ
Μρ![]() ±Θ§“‘PΓΔBΓΔDΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςABCœύΥΤΘ°
±Θ§“‘PΓΔBΓΔDΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςABCœύΥΤΘ°