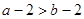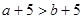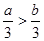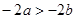题目内容
(8分)解下列不等式(组)并把解集表示在数轴上。
小题1:(1) ≥
≥ ; 小题2:(2)
; 小题2:(2)
小题1:(1)
 ≥
≥ ; 小题2:(2)
; 小题2:(2)
小题1:X≤ 2
小题2:-1<X≤2
此题考查一元一次不等式组的解法,把每个不等式解出后,在求出该不等式组的解集,可以通过数轴来求不等式组的解集;一元一次不等式的解法为:如果是分式先去分母,在不等式的两边公式乘以公分母,去分母时注意不等式的两边的每一项都乘以公分母;去分母后去括号,注意如果括号外面是负号,去括号是括号里面的每一项都要变号;去括号后移项,移项注意别忘了变号;移项后合并同类项,然后系数化为1,即在不等式的两边同时除以未知数的系数,注意如果是负数不等号要改变方向;
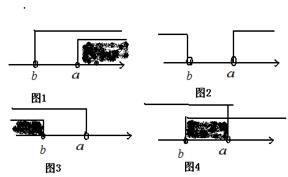
解集由以下四种情况,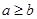 ,(1)当
,(1)当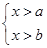 时,解集是
时,解集是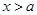 ;(2)当
;(2)当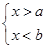 时,不等式无解集;(3)当
时,不等式无解集;(3)当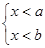 时,解集是
时,解集是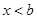 ;(4)当
;(4)当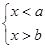 时,解集是
时,解集是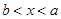 ;对于如下图(1)(2)(3)(4);
;对于如下图(1)(2)(3)(4);
解:小题1:(1)原不等式可以化为:
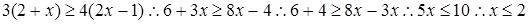 ;
;
小题2:(2)原不等式组可以化为: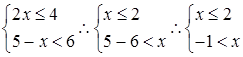 ,由上图(2)知,原不等式组的解集是:
,由上图(2)知,原不等式组的解集是: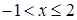 ;
;

解集由以下四种情况,
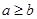 ,(1)当
,(1)当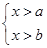 时,解集是
时,解集是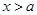 ;(2)当
;(2)当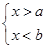 时,不等式无解集;(3)当
时,不等式无解集;(3)当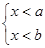 时,解集是
时,解集是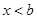 ;(4)当
;(4)当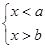 时,解集是
时,解集是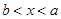 ;对于如下图(1)(2)(3)(4);
;对于如下图(1)(2)(3)(4);解:小题1:(1)原不等式可以化为:
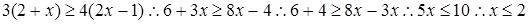 ;
;小题2:(2)原不等式组可以化为:
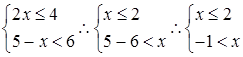 ,由上图(2)知,原不等式组的解集是:
,由上图(2)知,原不等式组的解集是: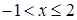 ;
;
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .现在要用含药率较高的同种灭虫药粉50kg和它混合.使混合后含药率大于30%而小于35%.则所用药粉的含药率x的范围是( )
.现在要用含药率较高的同种灭虫药粉50kg和它混合.使混合后含药率大于30%而小于35%.则所用药粉的含药率x的范围是( )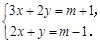 当m为何值时,x>y?
当m为何值时,x>y? 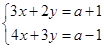 的解满足x>y,则a的取值范围是_________.
的解满足x>y,则a的取值范围是_________. >-
>-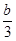
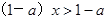 的解集是x<1,则a的范围是
的解集是x<1,则a的范围是 
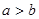 ,则下列结论一定错误的是
,则下列结论一定错误的是