题目内容
【题目】如图1,在平面直角坐标系中,![]() .
.
(1)求![]() 的面积;
的面积;
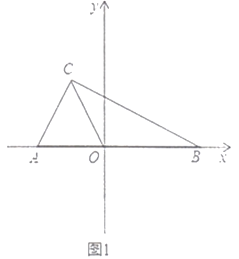
(2)点![]() 为坐标轴上一点,若
为坐标轴上一点,若![]() 的面积恰好是
的面积恰好是![]() 面积的一半,求点
面积的一半,求点![]() 的坐标.
的坐标.
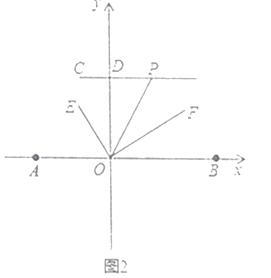
(3)如图2,过点![]() 作
作![]() 轴于点
轴于点![]() ,点
,点![]() 为
为![]() 延长线上的一动点,连接
延长线上的一动点,连接![]() 平分
平分![]() .当点
.当点![]() 运动时,
运动时,![]() 与
与![]() 度数之间的数量关系是否会改变?若不变,请直接写出其数量关系;若改变,请说明理由.
度数之间的数量关系是否会改变?若不变,请直接写出其数量关系;若改变,请说明理由.
【答案】(1)5;(2)![]() 或
或![]() (0,5)或(0,-5);(3)
(0,5)或(0,-5);(3)![]() 与
与![]() 度数之间的数量关系不变,
度数之间的数量关系不变,![]() .
.
【解析】
(1)根据三角形的面积公式计算即可.
(2)分两种情形分别构建方程即可解决问题.
(3)根据平行线的性质及证明∠1=∠3即可解决问题.
![]() 如图1,过点
如图1,过点![]() 作
作![]() 轴,重足为
轴,重足为![]()
![]() ,
,
![]() ,
,
![]()
![]() ;
;

![]() 如图1,过点
如图1,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]()
![]()
![]()
由![]() 知
知![]() ,
,
![]()
①当点![]() 在
在![]() 轴上时,设
轴上时,设![]()
![]()
![]()
解得:![]()
![]() 的坐标为
的坐标为![]()
②当点![]() 在
在![]() 轴上时,设
轴上时,设![]()
![]()
![]()
解得:![]()
![]() 的坐标为
的坐标为![]()
点![]() 的坐标为
的坐标为![]() 或
或![]()
(3)结论:∠OPD=2∠DOE.
理由:如图2,
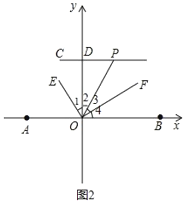
∵OE平分∠AOP,
∴∠AOE=∠POE=∠1+∠2,
∵OF⊥OE,
∴∠1+∠2+∠3=90°,∠4+∠AOE=90°,
∴∠3=∠4,
∵CD⊥y轴,
∴CD∥AB,
∴∠OPD=∠POB=2∠3,
∵∠1+∠2+∠3=90°,∠2+∠3+∠4=90°,
∴∠1+∠2+∠3=∠2+2∠3,
∴∠1=∠3,
由∠DOE=∠1,∠OPD=∠POB=2∠1
∴∠OPD=2∠DOE.

【题目】农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格x(元/千克) | 30 | 35 | 40 | 45 | 50 |
日销售量p(千克) | 600 | 450 | 300 | 150 | 0 |
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式;
(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
(3)若农经公司每销售1千克这种农产品需支出a元(a>0)的相关费用,当40≤x≤45时,农经公司的日获利的最大值为2430元,求a的值.(日获利=日销售利润﹣日支出费用)