题目内容
【题目】顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形①平行四边形;②菱形;③对角线互相垂直的四边形;④对角线相等的四边形,满足条件的是( )
A.①③④
B.②③
C.①②④
D.①②③
【答案】B
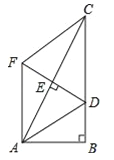
【解析】解:当AC⊥BD,E,F,G,H是AB,BC,CD,DA的中点,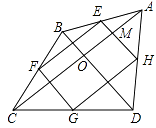
∵EH∥BD,FG∥BD,
∴EH∥FG,
同理;EF∥HG,
∴四边形EFGH是平行四边形.
∵AC⊥BD,
∴EH⊥EF,
∴四边形EFGH是矩形.
所以顺次连接对角线互相垂直的四边形各边的中点得到一个四边形是矩形,③符合题意.
而菱形的对角线互相垂直,则菱形符合题意,②符合题意,
平行四边形、对角线相等的四边形均不符合题意.
故选:B.
利用有一个角是直角的平行四边形是矩形,根据中点四边形的性质,顺次连接对角线互相垂直的四边形各边的中点得到一个四边形是矩形,据此判断即可.

练习册系列答案
相关题目