Question

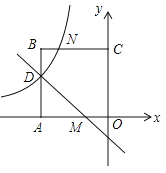
【题目】如图，在平面直角坐标系中，正方形OABC的顶点O与坐标原点重合，点C的坐标为（0，3），点A在x轴的负半轴上，点D、M分别在边AB、OA上，且AD=2DB，AM=2MO，一次函数y=kx+b的图象过点D和M，反比例函数的图象经过点D，与BC的交点为N．

（1）求反比例函数和一次函数的表达式；

（2）若点P在直线DM上，且使△OPM的面积与四边形OMNC的面积相等，求点P的坐标．

Answer 1

【答案】（1），y=﹣x﹣1；（2）P为（﹣10，9）或（8，﹣9）．

【解析】

试题分析：（1）由正方形OABC的顶点C坐标，确定出边长，及四个角为直角，根据AD=2DB，求出AD的长，确定出D坐标，代入反比例解析式求出m的值，再由AM=2MO，确定出MO的长，即M坐标，将M与D坐标代入一次函数解析式求出k与b的值，即可确定出一次函数解析式；

（2）把y=3代入反比例解析式求出x的值，确定出N坐标，得到NC的长，设P（x，y），根据△OPM的面积与四边形OMNC的面积相等，求出y的值，进而得到x的值，确定出P坐标即可．

试题解析：（1）∵正方形OABC的顶点C（0，3），∴OA=AB=BC=OC=3，∠OAB=∠B=∠BCO=90°，∵AD=2DB，∴AD=AB=2，∴D（﹣3，2），把D坐标代入得：m=﹣6，∴反比例解析式为，∵AM=2MO，∴MO=OA=1，即M（﹣1，0），把M与D坐标代入y=kx+b中得：，解得：k=b=﹣1，则直线DM解析式为y=﹣x﹣1；

（2）把y=3代入得：x=﹣2，∴N（﹣2，3），即NC=2，设P（x，y），∵△OPM的面积与四边形OMNC的面积相等，∴（OM+NC）OC=OM|y|，即|y|=9，解得：y=±9，当y=9时，x=﹣10，当y=﹣9时，x=8，则P坐标为（﹣10，9）或（8，﹣9）．