题目内容
【题目】如图,边长为 2 的正方形 OABC 顶点 O 与坐标原点 O 重合,边 OA、OC 分别与 x、y 正半轴重合, 在 x 轴上取点 P(﹣2,0),将正方形 OABC 绕点 O 逆时针旋转 a°(0°<a<180°),得到正方形 OA′B′C′,在旋转过程中,使得以 P,A′,B′为顶点的三角形是等腰三角形时,点 A′的坐标是_______.

【答案】(![]() ,1)或(0,2)或(1,
,1)或(0,2)或(1,![]() )或(
)或(![]() ,1)
,1)
【解析】
分四种情形:①当PB′=PA′时,②当A′与C重合时,③当PA′=A′B′时,④当PA′=PB′时,分别画出图形求解即可得到A′的坐标.
解:有四种情况:
①如图1中,当PB′=PA′时,连接PC′.易证△POC′是等边三角形,
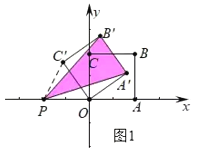
∴∠POA′=150°,∠A′OA=30°,
∵OA′=2,
∴A′(![]() ,1);
,1);
②如图2中,当A′与C重合时,△PA′B′是等腰三角形,此时A′(0,2);
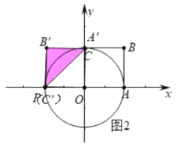
③如图3中,当PA′=A′B′时,△A′OP是等边三角形,
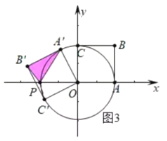
∴∠A′OP=60°,
∴A′(1,![]() );
);
④如图4中,当PA′=PB′时,易证△POC′是等边三角形,
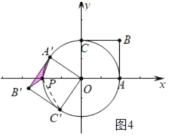
∴∠POC′=60°,
∵∠A′OC′=90°,
∴∠A′OP=30°,
∵OA′=2,
∴A′(![]() ,1),
,1),
综上所述,满足条件的点A′坐标为(![]() ,1)或(0,2)或(1,
,1)或(0,2)或(1,![]() )或(
)或(![]() ,1).
,1).
故答案为:(![]() ,1)或(0,2)或(1,
,1)或(0,2)或(1,![]() )或(
)或(![]() ,1).
,1).

练习册系列答案
相关题目