题目内容
14. 如图所示,已知在矩形ABCD中,对角线AC,BD交于点O,点P是AD上任意一点,PE⊥AC于点E,PF⊥BD于点F,AB=3,BC=4,则PE+PF的值是否会变化?若不变化,请加以证明;若变化,请说明理由.
如图所示,已知在矩形ABCD中,对角线AC,BD交于点O,点P是AD上任意一点,PE⊥AC于点E,PF⊥BD于点F,AB=3,BC=4,则PE+PF的值是否会变化?若不变化,请加以证明;若变化,请说明理由.
分析 首先连接OP.由矩形ABCD的两边AB=3,BC=4,可求得OA=OD=$\frac{5}{2}$,然后由S△AOD=S△AOP+S△DOP求得答案.
解答  解:不会变化;理由如下:
解:不会变化;理由如下:
连接OP,
∵矩形ABCD的两边AB=3,BC=4,
∴S矩形ABCD=AB•BC=12,OA=OC,OB=OD,AC=BD,AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5,
∴S△AOD=$\frac{1}{4}$S矩形ABCD=3,OA=OD=$\frac{5}{2}$,
∴S△AOD=S△AOP+S△DOP=$\frac{1}{2}$OA•PE+$\frac{1}{2}$OD•PF=$\frac{1}{2}$OA(PE+PF)=$\frac{1}{2}$×$\frac{5}{2}$×(PE+PF)=3,
∴PE+PF=$\frac{12}{5}$.
点评 此题考查了矩形的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4. 如图,a、b两个数在数轴上的位置如图所示,则下列各式正确的是( )
如图,a、b两个数在数轴上的位置如图所示,则下列各式正确的是( )
 如图,a、b两个数在数轴上的位置如图所示,则下列各式正确的是( )
如图,a、b两个数在数轴上的位置如图所示,则下列各式正确的是( )| A. | |a+b|=-a+b | B. | |a-b|=-a+b | C. | b-a<0 | D. | $\frac{a}{b}$>0 |
4.某数用科学记数法表示为a×106,下列说法正确的是( )
| A. | 1<|a|<6 | B. | 1≤|a|<6 | C. | 1<|a|<10 | D. | 1≤|a|<10 |
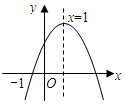 已知二次函数y=ax2+bx+c的图象如图所示,则点P(a,bc)在第二象限.
已知二次函数y=ax2+bx+c的图象如图所示,则点P(a,bc)在第二象限. 某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图),设这个苗圃园垂直于墙的一边长为x米.
某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图),设这个苗圃园垂直于墙的一边长为x米.