题目内容
【题目】如图,![]() ,在射线AN上取一点B,使
,在射线AN上取一点B,使![]() ,过点
,过点![]() 作
作![]() 于点C,点D是线段AB上的一个动点,E是BC边上一点,且
于点C,点D是线段AB上的一个动点,E是BC边上一点,且![]() ,设AD=x cm,BE=y cm,探究函数y随自变量x的变化而变化的规律.
,设AD=x cm,BE=y cm,探究函数y随自变量x的变化而变化的规律.

(1)取指定点作图.根据下面表格预填结果,先通过作图确定AD=2cm时,点E的位置,测量BE的长度。
①根据题意,在答题卡上补全图形;
②把表格补充完整:通过取点、画图、测量,得到了![]() 与
与![]() 的几组对应值,如下表:
的几组对应值,如下表:
|
|
| 2 | 3 |
|
|
|
| 2.9 | 3.4 | 3.3 | 2.6 | 1.6 | 0 |
(说明:补全表格时相关数值保留一位小数)
③建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(2)结合画出的函数图象,解决问题:当![]() 时,
时,![]() 的取值约为__________
的取值约为__________![]() .
.
【答案】见解析
【解析】
(1)①按题中要求借助于刻度尺和量角器规范的补全图形即可;②在所画图形中测量出BE的长度的近似值并填入表中的空格处即可;
(2)在方格纸中建立好平面直角坐标系,然后根据表中所给x与y的对应值描出相应的点,并将所描的点用“平滑的曲线”连接起来即可得到所求图象;
(3)由AD=BE可得y=x,由此可知所求的x的值是直线y=x与(2)中所画函数图象的交点的横坐标,故在(2)中建立的坐标系中画出直线y=x,即可由图象得到所求的x的值.
(1)①利用刻度尺、量角器在AN上截取AD=2cm,AB=6cm,过点B作BC⊥AM于点C,连接CD,作∠CDE=30°,DE交BC于点E,补全图形如下图所示:
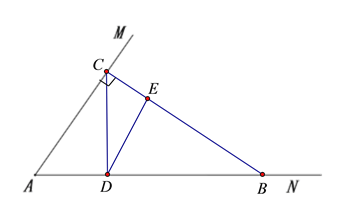
② 在①中所得图形中用刻度尺测量BE的长度得到BE的长度约为:3.5cm,将所得数据填入表格中补全表格如下:
|
|
| 2 | 3 |
|
|
|
| 2.9 | 3.4 | 3.5 | 3.3 | 2.6 | 1.6 | 0 |
③在方格纸中建立如下的坐标系,根据表格中的数据描点,连线,得到如下所示的y与x间的函数的图象(图中的黑色曲线):
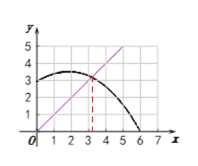
(3)由AD=BE可得y=x,
∴AD=BE时的x的取值是直线y=x与(1)中所画y与x的函数图象的交点的横坐标,
在(1)中所画的坐标系中画出直线y=x(如上图所示),由图可知直线y=x与(1)中所画的y与x的函数图象的交点的横坐标约为3.2,
∴当AD=BE时,x的取值约为3.2.