Question

【题目】如图，OB是∠AOC的平分线，OD是∠COE的平分线．

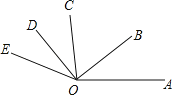
（1）若∠AOB＝40°，∠DOE＝30°，求∠BOD的度数；

（2）若∠AOD与∠BOD互补，且∠DOE＝35°，求∠AOC的度数．

Answer 1

【答案】（1）∠BOD＝70°；（2）∠AOC＝．

【解析】

（1）由图可知∠BOD＝∠COD+∠COB，根据角平分线的定义∠COD，∠COB的度数都可求，所以∠BOD的度数也可求.

（2）可设∠AOB＝x，然后利用角平分线的定义及∠DOE表示出∠AOD与∠BOD，然后利用∠AOD与∠BOD互补建立方程，解方程即可求出x的值，从而∠AOC的度数可求.

（1）∵OB是∠AOC的平分线，OD是∠COE的平分线

∴∠COB＝∠BOA＝40°，∠COD＝∠DOE＝30°

∴∠BOD＝∠COD+∠COB＝70°；

（2）由题意得：∠AOD+∠BOD＝180°，

∵OD平分∠COE，∠DOE＝35°，

∴∠COD＝∠DOE＝35°，

设∠AOB＝x，则∠AOD＝2x+35°，∠BOD＝x+35°，

∴2x+35°+x+35°＝180°，

解得：x＝ ，

∴∠AOC＝2x＝ ．