Question

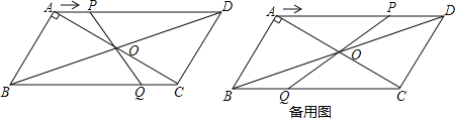
【题目】如图，在正方形内有一点满足，.连接、.

（1）求证：；

（2）求的度数.

Answer 1

【答案】（1）见解析；（2）15°

【解析】

（1）根据PB=PC得∠PBC=∠PCB，从而可得∠ABP=∠DCP，再利用SAS证明即可；

（2）由（1）得△PAD为等边三角形，可求得∠PAB=30°，∠PAC=∠PAD-∠CAD，因此可得结果．

解：（1）∵四边形ABCD为正方形，
∴∠ABC=∠DCB=90°，AB=CD，
∵BP=PC，
∴∠PBC=∠PCB，
∴∠ABP=∠DCP，
又∵AB=CD，BP=CP，

在△APB和△DPC中，

，
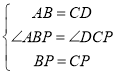∴△APB≌△DPC（SAS）；
（2）由（1）得AP=DP=AB=AD，

∴△PAD为等边三角形，

∴∠PAD=60°，∠PAB=30°，

在正方形ABCD中，∠BAC=∠DAC=45°，

∴∠PAC=∠PAD-∠CAD=60°-45°=15°.