��Ŀ����
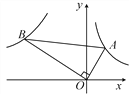
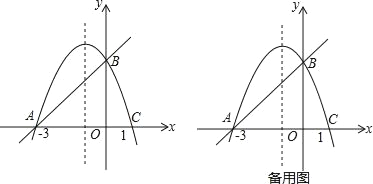
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y����x2+bx+c����A��B��C���㣬��֪��A����3��0����B��0��m����C��1��0����
��1����mֵ��
��2�����P��ֱ��AB�Ϸ�����������һ���㣨�����A��B�غϣ���
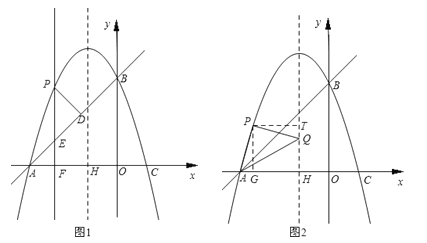
�ٹ���P��x��Ĵ��ߣ�����ΪF����ֱ��AB�ڵ�E����PD��AB�ڵ�D������P��ʲôλ��ʱ����PDE���ܳ���������ʱP������ꣻ
������AP������APΪ��������ֱ����APQ��������Qǡ�����������ߵĶԳ�����ʱ�������Ӧ�ĵ�P���꣮
���𰸡���1��m��ֵΪ3����2���ٵ�P����Ϊ����![]() ��
��![]() �����ڵ�P������Ϊ��
�����ڵ�P������Ϊ��![]() ��������1��
��������1��![]() ��2��������2��3��
��2��������2��3��
��������
��1��ֻ��ѵ�A��C���������y=��x2+bx+c���Ϳ���������ߵĽ���ʽ���Ϳ����m��ֵ��
��2�����á�PDE�ǵ���ֱ�������Σ�PE���ʱ��PDE���ܳ�������ô���ϵ�������ֱ��AB�Ľ���ʽ�����P�ĺ�����Ϊa�����E�ĺ�����ҲΪa�����P��E��������Ϳ���a�Ĵ���ʽ��ʾ��PE�ij���Ҳ�Ϳ�����a�Ĵ���ʽ��ʾ��Ȼ�����ö��κ�������ֵ�ԾͿ����PE�����PDE���ܳ����ʱ����P�����꣮
�ڵ���ֱ�ǡ�APQ�����߶������ǵױߣ��ʷ���������������ۣ�Ȼ����ȫ�������Σ��õ�����߶Σ�Ȼ����һ����ĸ��ʾһ���߶Σ��Ӷ�����P�������ø���ĸ��ʾ��Ȼ����������ߵĽ���ʽ���Ϳ������P�����꣮
��1����������y=��x2+bx+c������A����3��0����C��1��0������![]() ��
��
��ã�![]() ���������ߵĽ���ʽΪy=��x2��2x+3��
���������ߵĽ���ʽΪy=��x2��2x+3��
�ߵ�B��0��m����������y=��x2��2x+3�ϣ���m=3����m��ֵΪ3��
��2������ͼ1��
��OA=OB=3����AOB=90�㣬���AB0=45�㣮
��PF��OA��PD��AB�����PDA=��EFA=90��=��AOB����EF��OB�����PED=��ABO=45�㣬��PD=PEsin45��![]() PE��DE=PEcos45��
PE��DE=PEcos45��![]() PE�����PDE���ܳ�Ϊ��
PE�����PDE���ܳ�Ϊ��![]() 1��PE��
1��PE��
��ֱ��AB�Ľ���ʽΪy=mx+n������![]() ��
��
��ã�![]() ����ֱ��AB�Ľ���ʽΪy=x+3��
����ֱ��AB�Ľ���ʽΪy=x+3��
���P�ĺ�����Ϊa�����E�ĺ�����ҲΪa����yP=��a2��2a+3��yE=a+3����PE=yP��yE=����a2��2a+3������a+3��=��a2��3a=����a![]() ��2
��2![]() ��
��
�ߩ�1��0���൱a![]() ʱ��PEȡ�����ֵ����PDE���ܳ�Ҳ��ȡ�����ֵ��
ʱ��PEȡ�����ֵ����PDE���ܳ�Ҳ��ȡ�����ֵ��
��ʱyP=����![]() ��2��2����
��2��2����![]() ��+3
��+3![]() ���൱��P����Ϊ��
���൱��P����Ϊ��![]() ��ʱ����PDE���ܳ�ȡ�����ֵ��
��ʱ����PDE���ܳ�ȡ�����ֵ��
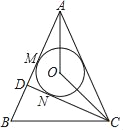
�ڢ���AQΪ����ֱ�ǡ�APQ�ĵױߣ���ͼ2������AP=PQ����APQ=90�㣮
����P��PG��OA������ΪG������P��PT��QH������ΪT��
�ߡ�PGH=��GHT=PTH=90�㣬���ı���PGHT�Ǿ��Σ����GPT=90�㣬PT=GH��PG=HT�����APG=90�㩁��GPQ=��TPQ��
�ڡ�AGP�͡�QTP�У�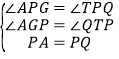 �����AGP�ա�QTP����AG=TQ��PG=PT����PG=GH��
�����AGP�ա�QTP����AG=TQ��PG=PT����PG=GH��
��������y=��x2��2x+3�ĶԳ���Ϊx![]() 1����OH=1��
1����OH=1��
��PG=t��t��0������OG=GH+OH=PG+OH=t+1��
�ߵ�P�ڵڶ����ޣ����P������Ϊ����t��1��t����
�ߵ�P��������y=��x2��2x+3�ϣ���t=������t��1��2��2����t��1��+3��
�����ã�t2+t��4=0��
��ã�t1![]() ����ȥ����t2
����ȥ����t2![]() �����P������Ϊ��
�����P��������![]() ����
����
����PQΪ����ֱ�ǡ�APQ�ĵױߣ���ͼ3������AP=AQ����PAQ=90�㣮
����P��PG��OA������ΪG�����С�APG=90�㩁��PAG=��HAQ��
�ڡ�AGP�͡�QHA�У�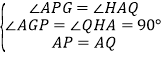 �����AGP�ա�QHA����PG=AH��
�����AGP�ա�QHA����PG=AH��
��AH=AO��OH=3��1=2����PG=2����yP=2��
�⩁x2��2x+3=2�ã�x1=��1![]() ��x2=��1
��x2=��1![]() ��
��
�ߵ�P�ڵڶ����ޣ����P������Ϊ����1![]() ��2����
��2����
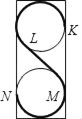
����APΪ����ֱ�ǡ�APQ�ĵױߣ���ͼ4������AQ=PQ����AQP=90�㣮
����P��PT��QH������ΪT�����С�AQH=90�㩁��PQT=��TPQ��
�ڡ�AHQ�͡�QTP�У��ߡ�AQH=��TPQ����AHQ=��QTP��QA=QP�����AHQ�ա�QTP����AH=QT��QH=PT��
��AH=2����QT=2��
��QH=PT=p��p��0������TH=p+2��
�ߵ�P�ڵڶ����ޣ����P������Ϊ����p��1��p+2����
�ߵ�P��������y=��x2��2x+3�ϣ���p+2=������p��1��2��2������p��1��+3��
�����ã�p2+p��2=0��
��ã�p1=��2����ȥ����p2=1�����P������Ϊ����2��3����
������������P��������![]() ��������1
��������1![]() ��2��������2��3����
��2��������2��3����

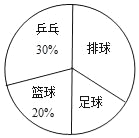
����Ŀ��ijУΪ�˵�����꼶ѧ���μ���ƹ���������������������������������������������������ѧУ�Ӱ��꼶�����ȡ�˲���ѧ�����е��飬���ݵ��������������²�������ͳ�Ʊ���ͳ��ͼ��
��� | Ƶ���������� | Ƶ�� |
ƹ�� | a | 0.3 |
���� | 20 | |
���� | 15 | b |
���� | ||
�ϼ� | c | 1 |
�������������Ϣ������и��⣺
��1��a���� ����b���� ����c���� ����
��2��������ͳ��ͼ�У���������Ӧ��Բ�Ľ����� ���ȣ�
��3������У���꼶����600��ѧ�����Թ��Ƹ�У���꼶ϲ���������������