题目内容
【题目】如图,在平面直角坐标系xOy中,已知正比例函数 ![]() 与一次函数
与一次函数 ![]() 的图像交于点A.
的图像交于点A.
(1)求点A的坐标;
(2)设x轴上一点P(a,b),过点P作x轴的垂线(垂线位于点A的右侧),分别交 ![]() 和
和 ![]() 的图像于点B、C,连接OC,若BC=
的图像于点B、C,连接OC,若BC= ![]() OA,求△OBC的面积.
OA,求△OBC的面积.
【答案】
(1)解:由题意得, 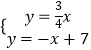 ,解得
,解得 ![]() ,
,
∴点A的坐标为(4,3)
(2)解:过点A作x轴的垂线,垂足为D,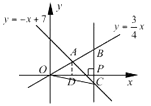
在Rt△OAD中,由勾股定理得,![]() ,
,
∴ ![]() .
.
∵P(a,0),∴B(a, ![]() ),C(a,-a+7),∴BC=
),C(a,-a+7),∴BC= ![]() ,
,
∴ ![]() ,解得a=8.
,解得a=8.
∴ ![]() .
.
【解析】(1)将两函数解析式联立方程组,解方程组求出x、y的值,即可得出点A的坐标。
(2)过点A作x轴的垂线,垂足为D,可知点、C、B的横坐标相同,因此先根据勾股定理求出OA的长,根据BC= ![]() OA,求出BC的长,再设P(a,0),分别表示出点B、C的坐标,用含a的代数式求出BC,再根据BC=7建立关于a的方程,求解得出a的值,然后求出△OBC的面积即可。
OA,求出BC的长,再设P(a,0),分别表示出点B、C的坐标,用含a的代数式求出BC,再根据BC=7建立关于a的方程,求解得出a的值,然后求出△OBC的面积即可。

【题目】下列命题中,假命题是( )
A. 对顶角相等
B. 等角的补角相等
C. 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行
D. 如果一个角的两边分别平行于另一个角的两边,那么这两个角相等
【题目】为了强化司机的交通安全意识,我市利用交通安全宣传月对司机进行了交通安全知识问卷调查.关于酒驾设计了如下调查问卷:
克服酒驾﹣﹣你认为哪种方式最好?(单选) |
A加大宣传力度,增强司机的守法意识. B在汽车上张贴温馨提示:“请勿酒驾”. C司机上岗前签“拒接酒驾”保证书. D加大检查力度,严厉打击酒驾. E查出酒驾追究一同就餐人的连带责任. |
随机抽取部分问卷,整理并制作了如下统计图:

根据上述信息,解答下列问题:
(1)本次调查的样本容量是多少?
(2)补全条形图,并计算B选项所对应扇形圆心角的度数;
(3)若我市有3000名司机参与本次活动,则支持D选项的司机大约有多少人?

